Statistics

Problem Statement for "CellRemoval"

Problem Statement

In biology, organisms have the following property: Starting from the first cell (the zygote), each cell during an organism's development process either divides into 2 other cells or does not divide at all. An organism is mature when all of its cells will not divide any further.

Let's assign a unique number to each cell in an organism's development process. For example, consider a species in which each organism starts with cell 0, which divides into cells 1 and 2. Cell 1 divides into cells 3 and 4. Cells 2, 3 and 4 do not divide. Every mature organism of this species will consist of exactly 3 cells - 2, 3 and 4.

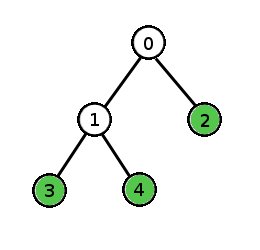
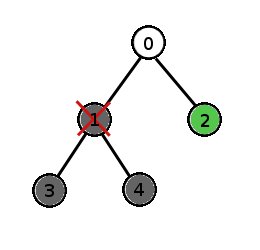
During the development process, if we kill a cell, it will be absent in the mature form of the organism. If that cell happens to be a cell that divides, then the mature organism will be missing all of the cell's descendants as well because the cell is killed before it has a chance to divide. For example, in the organism described above, if we kill cell 1 during the development process, the mature organism will contain only cell 2.

You are given a int[] parentCell describing the development process of an organism. The i-th element of parentCell is the parent cell of cell i (where i is a 0-based index). The zygote's parent is -1. Return the number of cells the mature form of this organism would have if you killed cell deletedCell during the development process.

Definition

Class:
CellRemoval
Method:
cellsLeft
Parameters:
int[], int
Returns:
int
Method signature:
int cellsLeft(int[] parent, int deletedCell)
(be sure your method is public)

Constraints

  • parentCell will contain exactly N elements, where N is an odd integer between 1 and 50, inclusive.
  • There will be exactly one "-1" element in parentCell.
  • Every element of parentCell will be between -1 and N-1, inclusive.
  • parentCell will form a binary tree.
  • deletedCell will be between 0 and N-1, inclusive.

Examples

  1. {-1}

    0

    Returns: 0

  2. {-1,0,0}

    0

    Returns: 0

  3. {-1,0,0}

    1

    Returns: 1

  4. {1,-1,1}

    2

    Returns: 1

  5. {2,2,-1}

    2

    Returns: 0

  6. {-1,0,0,1,1}

    2

    Returns: 2

    This is the example organism from the problem statement. If we kill cell 2, there will still be two cells left (3 and 4).

  7. {-1,0,0,1,1}

    1

    Returns: 1

    This is the example organism from the problem statement. If we kill cell 1, the only cell left will be cell 2. Cells 3 and 4 will not exist because cell 1 is their ancestor.

  8. {-1,0,0,1,1}

    0

    Returns: 0

    If we kill the zygote, there is nothing left.

  9. {6,5,6,-1,3,3,5}

    0

    Returns: 3

  10. {2,6,-1,4,2,6,4}

    6

    Returns: 2

  11. {5,3,6,6,3,-1,5}

    3

    Returns: 2

  12. {6,6,5,1,1,-1,5}

    0

    Returns: 3

  13. {4,0,4,0,-1}

    2

    Returns: 2

  14. {-1,4,3,0,5,0,4,5,3}

    0

    Returns: 0

  15. {6,6,5,0,5,0,8,8,-1}

    7

    Returns: 4

  16. {8,7,0,5,5,8,7,0,-1}

    1

    Returns: 4

  17. {-1,0,6,0,1,6,1}

    0

    Returns: 0

  18. {6,-1,1,2,2,1,5,6,5}

    2

    Returns: 3

  19. {2,0,3,-1,0,6,3,2,6}

    4

    Returns: 4

  20. {-1,0,0,2,2}

    3

    Returns: 2

  21. {8,4,0,4,8,-1,5,0,5}

    4

    Returns: 3

  22. {3,2,4,2,-1,7,7,4,3}

    1

    Returns: 4

  23. {2,3,-1,5,5,2,3}

    2

    Returns: 0

  24. {1,4,1,5,-1,4,5}

    4

    Returns: 0

  25. {3,0,0,-1,3,2,2}

    0

    Returns: 1

  26. {3,-1,6,1,6,3,1}

    4

    Returns: 3

  27. {1,5,1,7,7,-1,5,6,6}

    8

    Returns: 4

  28. {6,0,6,-1,2,2,3,3,0}

    3

    Returns: 0

  29. {8,4,4,5,-1,1,8,1,5}

    3

    Returns: 4

  30. {2,2,4,4,-1}

    0

    Returns: 2

  31. {6,7,6,7,8,1,8,-1,1}

    3

    Returns: 4

  32. {4,2,4,2,-1}

    1

    Returns: 2

  33. {1,-1,0,1,0}

    2

    Returns: 2

  34. {5,3,8,8,2,2,5,3,-1}

    7

    Returns: 4

  35. {3,5,3,-1,0,0,5}

    4

    Returns: 3

  36. {1,3,1,-1,3}

    0

    Returns: 2

  37. {7,7,6,1,6,-1,5,5,1}

    4

    Returns: 4

  38. {2,2,8,8,-1,6,4,6,4}

    8

    Returns: 2

  39. {24,42,4,30,29,43,22,15,26,36,26,16,3,22,21,41,18,16,34,41,12,29,32,30,43,15,4,38,36,-1,24,42,18,6,21,38,6,17,32,17,3,34,12,14,14}

    24

    Returns: 17

  40. {-1,4,36,24,10,29,19,31,7,0,26,31,4,18,7,6,14,24,23,0,29,14,10,35,26,1,19,1,9,36,18,6,22,35,22,9,23}

    35

    Returns: 13

  41. {38,20,34,7,6,37,5,8,10,30,6,37,20,2,16,7,21,23,22,23,8,33,11,21,4,30,15,34,16,15,10,36,38,5,4,33,11,-1,22,2,36}

    39

    Returns: 20

  42. {9,14,13,2,2,-1,14,9,13,11,11,5,10,5,10}

    10

    Returns: 5

  43. {-1,21,24,30,46,1,16,29,30,41,18,33,26,31,12,45,29,7,16,45,27,32,41,18,35,6,9,1,19,32,22,33,0,9,6,0,12,19,21,35,46,24,31,27,26,22,7}

    28

    Returns: 23

  44. {31,4,11,11,16,2,17,26,26,6,4,33,8,9,15,3,32,31,16,2,9,12,33,22,15,22,13,32,37,12,3,-1,0,17,37,0,8,13,6}

    35

    Returns: 19

  45. {32,24,5,30,16,19,19,9,-1,12,31,21,14,24,4,35,8,27,8,30,21,34,35,31,18,17,9,4,17,18,12,14,16,32,5,27,34}

    0

    Returns: 18

  46. {10,10,-1,5,2,8,4,5,4,8,2}

    10

    Returns: 4

  47. {26,29,-1,1,2,26,15,31,20,5,29,25,4,20,25,2,3,3,27,32,6,1,14,5,32,4,14,31,6,12,27,12,15}

    6

    Returns: 14

  48. {4,19,16,14,11,4,11,0,14,2,19,-1,6,7,6,3,3,16,7,2,0}

    16

    Returns: 7

  49. {1,4,5,9,11,11,12,18,13,1,18,-1,9,5,13,4,3,12,3}

    17

    Returns: 9

  50. {19,13,27,22,20,24,34,13,1,10,6,30,15,5,30,6,21,34,15,-1,5,25,1,21,19,20,12,24,0,25,12,10,22,0,27}

    27

    Returns: 10

  51. {18,-1,24,0,31,23,2,34,2,29,5,32,29,14,10,32,22,18,1,34,28,24,31,1,20,22,14,11,23,10,28,11,5,0,20}

    14

    Returns: 16

  52. {13,10,1,9,-1,1,7,4,2,2,4,9,13,10,15,7,15}

    8

    Returns: 8

  53. {14,0,14,7,-1,6,10,4,5,10,0,2,5,6,4,2,7}

    7

    Returns: 7

  54. {3,3,11,22,22,7,15,12,19,19,24,12,16,7,2,23,-1,14,2,23,15,24,11,16,14}

    15

    Returns: 11

  55. {32,19,7,17,27,34,1,6,2,2,21,30,5,9,19,7,6,-1,33,31,30,27,9,28,16,16,24,33,38,28,5,3,21,1,17,31,24,32,34,38,3}

    22

    Returns: 20

  56. {17,7,13,16,13,15,16,5,15,0,7,3,8,3,0,-1,8,5,17}

    0

    Returns: 8

  57. {23,18,33,32,27,2,7,28,-1,8,13,33,1,12,11,23,11,6,28,0,27,18,1,6,32,12,7,21,8,2,13,17,17,21,0}

    4

    Returns: 17

  58. {25,34,34,27,21,21,24,36,31,2,27,8,26,8,9,35,38,30,23,26,36,9,24,31,15,1,0,30,0,35,25,38,-1,18,32,1,23,2,32,18,15}

    0

    Returns: 18

  59. {-1,0,1,11,15,2,8,6,0,2,11,8,1,3,3,6,15}

    15

    Returns: 7

  60. {13,15,14,10,5,9,14,21,9,19,-1,16,3,19,5,22,15,3,0,16,0,22,10,13,21}

    18

    Returns: 12

  61. {11,17,11,5,18,23,18,23,22,0,20,22,0,20,21,-1,8,2,5,2,21,15,15,8,17}

    0

    Returns: 11

  62. {7,4,5,12,11,6,12,6,4,5,11,7,-1}

    8

    Returns: 6

  63. {3,31,28,47,16,18,18,21,41,8,46,45,47,43,10,31,36,2,26,33,3,42,15,2,41,6,19,36,26,23,8,28,45,-1,25,43,19,33,46,21,16,23,44,25,6,44,42,15,10}

    22

    Returns: 24

  64. {1,4,3,4,-1,1,8,3,2,8,2}

    3

    Returns: 2

  65. {17,25,0,14,7,2,5,25,18,8,16,27,10,9,19,7,31,31,19,0,8,14,9,17,18,2,30,16,30,10,5,-1,27}

    19

    Returns: 11

  66. {7,5,-1,11,11,10,1,10,13,7,2,2,4,1,4,5,13}

    11

    Returns: 6

  67. {2,8,12,8,5,-1,7,5,4,3,12,9,4,3,9,2,7}

    13

    Returns: 8

  68. {4,9,14,2,14,10,10,2,3,11,3,4,9,11,-1}

    0

    Returns: 7

  69. {8,11,8,5,29,4,15,28,29,0,17,9,10,26,10,26,3,4,25,5,15,17,18,28,9,-1,25,11,0,18,3}

    0

    Returns: 11

  70. {9,27,21,13,13,31,30,19,5,25,22,29,15,8,5,21,15,18,11,28,19,30,9,1,29,6,11,6,2,27,31,-1,2,8,18,25,28,24,22,1,24}

    24

    Returns: 19

  71. {30,26,15,10,18,26,20,17,21,14,9,30,15,11,20,6,8,14,8,18,-1,23,3,9,10,23,11,21,3,17,6}

    23

    Returns: 11

  72. {11,2,15,6,0,15,11,17,9,4,9,14,2,4,-1,14,17,0,6,3,3}

    4

    Returns: 8

  73. {-1,5,0,8,14,6,2,9,0,2,5,6,8,3,3,14,9}

    14

    Returns: 7

  74. {-1,0,1,13,1,6,13,3,0,2,2,8,6,8,3}

    5

    Returns: 7

  75. {5,4,0,10,5,-1,8,8,0,10,4}

    1

    Returns: 5

  76. {21,25,28,29,31,21,13,29,10,8,28,16,32,0,17,26,10,18,31,18,19,12,8,17,13,16,0,19,32,25,26,12,-1}

    1

    Returns: 16

  77. {3,8,9,2,6,6,9,8,2,-1,3}

    8

    Returns: 4

  78. {5,19,4,37,5,33,29,11,4,38,11,29,30,17,34,33,30,20,8,18,8,18,0,20,26,37,2,19,34,0,25,25,38,-1,6,26,17,2,6}

    37

    Returns: 16

  79. {17,21,-1,30,31,2,35,29,4,42,33,36,4,29,45,32,8,40,24,48,45,24,27,25,5,42,14,14,36,21,25,2,40,5,8,30,37,20,35,48,20,37,33,32,41,31,17,41,27}

    13

    Returns: 24

  80. {1,4,-1,26,2,1,7,20,6,10,3,3,8,2,20,6,17,26,14,10,13,4,14,17,7,8,13}

    13

    Returns: 3

  81. {28,6,0,16,9,18,27,15,13,34,6,18,19,-1,9,19,8,0,1,32,4,1,4,28,32,34,27,13,15,26,3,26,8,3,16}

    8

    Returns: 6

  82. {26,18,29,28,28,16,29,19,26,-1,8,9,11,31,16,13,32,10,19,12,10,32,0,13,31,8,12,24,18,11,9,0,24}

    24

    Returns: 13

  83. {11,37,24,29,19,14,24,3,39,27,11,13,33,4,30,-1,21,3,15,39,40,35,29,14,8,18,20,18,21,25,15,20,4,35,13,19,37,40,25,30,8,27,33}

    15

    Returns: 0

  84. {19,15,18,0,16,24,29,39,11,29,19,23,35,10,37,14,30,36,26,41,24,11,33,26,39,37,14,32,33,18,25,4,36,23,35,15,10,-1,4,41,30,25,16,32,0}

    2

    Returns: 22

  85. {10,6,7,15,15,10,0,6,5,3,-1,5,8,7,0,8,3}

    7

    Returns: 7

  86. {9,27,29,25,2,6,0,19,27,20,7,2,19,0,3,7,21,6,5,23,-1,23,3,20,21,5,29,18,18,9,25}

    16

    Returns: 15

  87. {16,-1,5,17,12,21,22,13,23,23,17,24,5,1,12,19,22,25,10,30,10,13,24,30,19,1,16,21,2,2,25}

    30

    Returns: 9

  88. {10,5,10,0,0,3,3,6,6,5,-1}

    7

    Returns: 5

  89. {25,26,34,16,37,31,23,17,18,38,1,18,38,16,23,28,29,28,-1,1,32,32,29,17,3,22,11,25,22,11,3,13,8,37,13,8,34,31,26}

    34

    Returns: 18

  90. {-1,38,27,26,25,0,1,23,1,36,4,7,5,11,29,5,7,29,38,13,4,27,16,18,23,22,22,24,24,26,31,18,31,13,36,25,11,16,0}

    23

    Returns: 6

  91. {1,12,19,1,2,7,22,2,13,0,22,9,17,17,12,13,7,19,4,-1,4,0,9}

    3

    Returns: 11

  92. {7,11,21,12,22,6,16,6,9,21,7,12,0,23,1,5,-1,5,9,16,0,23,11,1,22}

    16

    Returns: 0

  93. {31,31,3,32,30,18,40,33,10,20,37,40,33,22,26,22,5,25,37,41,11,34,26,27,41,28,10,28,32,30,18,3,8,25,8,27,39,-1,11,5,39,34,20}

    14

    Returns: 21

  94. {13,3,18,34,6,30,3,32,37,21,40,23,39,31,0,24,37,0,38,22,22,23,24,12,6,21,40,1,13,35,38,32,34,12,-1,30,1,35,39,31,18}

    27

    Returns: 20

  95. {42,34,28,48,7,12,33,20,30,16,32,16,6,32,5,39,-1,20,5,23,12,33,9,6,40,28,9,26,34,7,27,11,27,30,11,48,39,42,40,19,3,10,10,3,19,41,41,23,26}

    17

    Returns: 24

  96. {30,27,7,30,18,32,2,27,4,8,6,2,31,22,7,8,17,4,-1,25,6,19,32,16,16,18,29,17,29,19,31,22,25}

    27

    Returns: 12

  97. {11,9,16,8,8,9,15,16,11,12,15,14,14,2,2,12,-1}

    6

    Returns: 8

  98. {2,33,3,14,8,7,3,21,2,13,31,30,36,6,-1,9,34,13,6,4,9,26,34,21,29,29,8,33,7,26,36,30,31,0,14,4,0}

    18

    Returns: 18

  99. {2,5,3,1,46,22,2,39,44,16,4,-1,44,5,28,3,19,31,8,35,16,39,11,32,41,30,17,1,38,17,32,12,8,31,35,12,22,11,36,46,30,38,19,4,28,36,41}

    11

    Returns: 0

  100. {5,7,28,17,5,10,20,9,25,14,19,27,19,11,26,7,10,22,20,28,9,11,25,22,27,14,-1,17,26}

    8

    Returns: 14

  101. {20,25,5,18,16,8,1,20,3,11,25,7,18,2,32,13,3,0,-1,16,8,32,0,13,1,5,7,15,2,11,17,15,17}

    24

    Returns: 16

  102. {9,19,22,30,16,6,13,18,19,31,2,23,17,-1,23,24,11,29,31,18,6,29,11,13,14,30,24,2,17,22,9,14,16}

    15

    Returns: 16

  103. {10,5,3,10,5,9,9,12,12,3,11,-1,11}

    0

    Returns: 6

  104. {7,23,18,19,12,14,2,13,12,8,13,3,0,-1,0,11,8,14,11,7,2,19,18,3,23}

    15

    Returns: 12

  105. {32,6,39,28,28,15,5,23,20,34,3,38,3,29,39,4,23,15,9,13,13,36,31,32,20,35,18,12,34,-1,31,18,36,38,29,9,4,5,12,35,6}

    18

    Returns: 18

  106. {3,10,12,-1,17,13,42,0,46,3,24,9,40,17,37,39,29,11,13,43,34,2,21,40,23,42,36,23,34,21,37,6,10,39,31,12,31,46,6,43,9,29,0,11,36,2,24}

    18

    Returns: 23

  107. {-1,8,11,26,14,12,8,10,30,30,0,13,10,36,3,35,7,11,26,7,32,25,28,20,35,12,36,14,13,25,32,16,0,28,16,3,20}

    22

    Returns: 18

  108. {11,9,0,12,7,10,12,1,6,-1,24,15,23,15,24,9,23,10,7,8,1,0,6,11,8}

    15

    Returns: 3

  109. {-1,0,0,2,2,4,4,6,6}

    4

    Returns: 2

  110. {26,2,32,36,40,19,43,24,30,13,21,14,24,21,19,4,30,10,44,12,7,32,17,43, 35,18,7,36,10,16,5,38,35,4,13,-1,16,26,1,12,2,5,18,40,1,17,38,44,14}

    24

    Returns: 14

  111. {30,-1,18,45,5,1,23,4,42,6,47,33,27,23,33,18,34,0,34,32,6,35,20,37,44,27,7,2,4,42,3,7,3,20,5,45,30,10,2,44,43,0,10,1,35,47,32,43,37}

    2

    Returns: 22

  112. {28,35,9,43,32,12,38,5,1,22,6,9,43,41,21,18,34,20,14,3,4,-1,45,6,2,28,18,5,3,26,4,21,26,31,45,12,20,34,35,1,2,38,10,14,22,32,41,10,31}

    42

    Returns: 24

  113. {29,22,29,33,6,35,10,43,20,7,14,27,4,39,1,18,18,24,8,2,32,41,38,44,33,35,2,24,27,20,4,45,42,41,1,6,45,32,-1,14,39,43,38,42,22,44,7,10,8}

    11

    Returns: 24

  114. {27,16,8,29,0,39,46,43,-1,3,4,43,27,7,41,46,13,30,44,11,13,24,25,4,8,21,24,26,2,7,26,21,17,16,31,29,30,31,39,25,11,28,0,2,41,3,44,28,17}

    46

    Returns: 23

  115. {-1, 0, 0, 1, 1 }

    1

    Returns: 1

  116. {26, 2, 32, 36, 40, 19, 43, 24, 30, 13, 21, 14, 24, 21, 19, 4, 30, 10, 44, 12, 7, 32, 17, 43, 35, 18, 7, 36, 10, 16, 5, 38, 35, 4, 13, -1, 16, 26, 1, 12, 2, 5, 18, 40, 1, 17, 38, 44, 14 }

    24

    Returns: 14

  117. {1, -1, 1 }

    0

    Returns: 1

  118. {26, 2, 32, 36, 40, 19, 43, 24, 30, 13, 21, 14, 24, 21, 19, 4, 30, 10, 44, 12, 7, 32, 17, 43, 35, 18, 7, 36, 10, 16, 5, 38, 35, 4, 13, -1, 16, 26, 1, 12, 2, 5, 18, 40, 1, 17, 38, 44, 14 }

    35

    Returns: 0

  119. {2, 2, -1 }

    2

    Returns: 0

  120. {-1, 3, 3, 0, 0 }

    3

    Returns: 1

  121. {1, -1, 1 }

    2

    Returns: 1

  122. {26, 2, 32, 36, 40, 19, 43, 24, 30, 13, 21, 14, 24, 21, 19, 4, 30, 10, 44, 12, 7, 32, 17, 43, 35, 18, 7, 36, 10, 16, 5, 38, 35, 4, 13, -1, 16, 26, 1, 12, 2, 5, 18, 40, 1, 17, 38, 44, 14 }

    0

    Returns: 24

  123. {-1, 0, 0 }

    1

    Returns: 1

  124. {2, 2, 4, 4, -1 }

    4

    Returns: 0

  125. {1, -1, 1, 0, 0 }

    0

    Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: