Statistics

Problem Statement for "HexagonalBattlefieldEasy"

Problem Statement

You may have heard of the game "Heroes of Might and Magic". Recently, battles in this game have been broadcast online, and the weekly battles between Petr and Vasyl have been very popular. Petr usually wins these battles, so Vasyl has decided to develop a new strategy.


The battlefield in this game consists of equal hexagonal cells arranged in the form of a larger hexagon. The number of cells on each side of the battlefield represents the size of the field. The coordinate system is shown in the following figure, which depicts a battlefield of size 3:

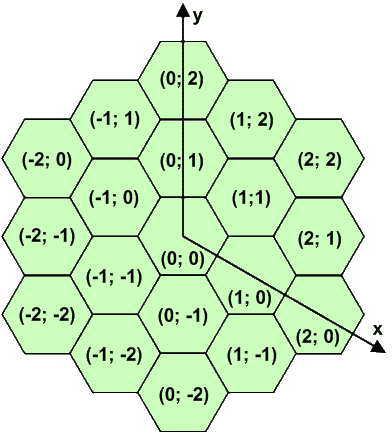
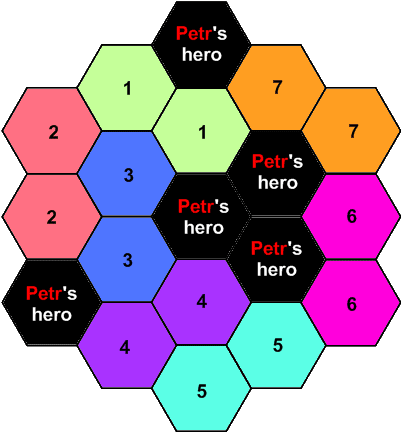
This week, Petr and Vasyl are playing on a battlefield of size N. Some of the cells are already occupied by Petr's heroes. The locations of these cells are given in the int[]s X and Y, where (X[i], Y[i]) is the location of Petr's i-th hero. To defeat Petr, Vasyl must occupy every single free cell with his own heroes. Unfortunately, Vasyl only has equestrian heroes, each of which occupy exactly two adjacent cells. No two heroes can occupy a single cell. One possible correct arrangement is shown in the following figure:

Vasyl wants to simulate a battle with every possible arrangement of his heroes so that he can determine the optimal one. Return the number of different possible arrangements he will consider.

Definition

Class:
HexagonalBattlefieldEasy
Method:
countArrangements
Parameters:
int[], int[], int
Returns:
int
Method signature:
int countArrangements(int[] X, int[] Y, int N)
(be sure your method is public)

Constraints

  • N will be between 1 and 4, inclusive.
  • X will contain between 1 and 50 elements, inclusive.
  • X and Y will each contain the same number of elements.
  • All points (X[i], Y[i]) will lie inside the battlefield of size N.
  • All points (X[i], Y[i]) will be distinct.

Examples

  1. {-2,0,1,1,0}

    {-2,0,1,0,2}

    3

    Returns: 10

    This is the battlefield shown in the figure above.

  2. {0}

    {0}

    2

    Returns: 2

  3. {0}

    {0}

    3

    Returns: 104

  4. {-1,0,0,1,2}

    {0,0,1,0,0}

    3

    Returns: 6

  5. {0,0}

    {0,-1}

    2

    Returns: 0

  6. {0,0}

    {0,1}

    2

    Returns: 0

  7. {0,-1}

    {0,0}

    2

    Returns: 0

  8. {0,1}

    {0,0}

    2

    Returns: 0

  9. {-1,0,1}

    {-1,0,1}

    2

    Returns: 1

  10. {0,0,0}

    {-1,0,1}

    2

    Returns: 1

  11. {1,0,-1}

    {0,0,0}

    2

    Returns: 1

  12. {-1,0,1}

    {-1,0,1}

    2

    Returns: 1

  13. {-1,1,0}

    {0,1,-1}

    2

    Returns: 0

  14. {-1,1,0}

    {-1,0,1}

    2

    Returns: 0

  15. {-1,0,0}

    {-1,-1,1}

    2

    Returns: 1

  16. {1,1,-1}

    {1,0,0}

    2

    Returns: 1

  17. {0,1,1,0,-1}

    {1,1,0,-1,-1}

    2

    Returns: 1

  18. {-1,0,1}

    {0,1,1}

    2

    Returns: 2

  19. {1,1,0}

    {1,0,-1}

    2

    Returns: 2

  20. {0,-1,-1}

    {-1,-1,0}

    2

    Returns: 2

  21. {0,-1,-1,0,1,1}

    {1,0,-1,-1,0,1}

    2

    Returns: 0

  22. {0,0,1,1,0,-1,-1}

    {0,-1,0,1,1,0,-1}

    3

    Returns: 2

  23. {-2,-1,0,1,2}

    {0,0,0,0,0}

    3

    Returns: 0

  24. {-2,-1,0,1,2,-2,2}

    {0,0,0,0,0,-1,1}

    3

    Returns: 9

  25. {0,0,0,0,0,-1,1}

    {-2,-1,0,1,2,-1,1}

    3

    Returns: 4

  26. {-1,0,1}

    {-1,0,1}

    3

    Returns: 18

  27. {1,0,-1,-1,0,1,1,0,-1,0,0}

    {2,2,1,0,0,0,-1,-2,-2,-1,1}

    3

    Returns: 1

  28. {-2,-1,0,1,2,1,-1,-2,2,2,-2}

    {-1,0,0,0,1,-1,1,0,0,2,-2}

    3

    Returns: 4

  29. {-2,-1,0,1,2,2,2,1,0,-1,-2,-2,0}

    {0,1,2,2,2,1,0,-1,-2,-2,-2,-1,0}

    3

    Returns: 2

  30. {0,1,2,-2,-1,0,0}

    {2,2,2,-2,-2,-2,0}

    3

    Returns: 13

  31. {0,0,0,-1,-2,1,2}

    {-2,-1,0,0,0,1,2}

    3

    Returns: 8

  32. {0}

    {0}

    4

    Returns: 78408

  33. {0,-1,0,1,1,0,-1}

    {0,-1,-1,0,1,1,0}

    4

    Returns: 1940

  34. {0,0,0,0,-1,-2,-3,1,2,3,1,0,-1}

    {0,-1,-2,-3,0,0,0,1,2,3,0,1,-1}

    4

    Returns: 64

  35. {1,0,-1,-1,0,1,1,0,-1}

    {2,2,1,0,0,0,-1,-2,-2}

    4

    Returns: 50

  36. {0,0,0,0,0}

    {3,2,1,0,-1}

    4

    Returns: 3500

  37. {0,0,0,0,0}

    {-3,-2,-1,0,1}

    4

    Returns: 3500

  38. {-1,-1,-1,-1,2,2,2,2,0}

    {0,-1,-2,-3,3,2,1,0,1}

    4

    Returns: 63

  39. {3,3,3,3,2,1,0,-1,-2,-3,-3,-3,-3,-2,-1,0,1,2,-1,-1,0,1,1,0}

    {3,2,1,0,-1,-2,-3,-3,-3,-3,-2,-1,0,1,2,3,3,3,0,-1,-1,0,1,1}

    4

    Returns: 0

  40. {0,-1,-1,0,1,1,0,0,-1,-2,-3,-3,-3,-3,-2,-1,0,1,2,3,3,3,3,2,1}

    {1,0,-1,-1,0,1,0,3,2,1,0,-1,-2,-3,-3,-3,-3,-2,-1,0,1,2,3,3,3}

    4

    Returns: 2

  41. {3,-3,0,3,0,-3,0}

    {0,0,3,3,-3,-3,0}

    4

    Returns: 4732

  42. {0,0,2,-2,2}

    {-1,2,2,-1,-1}

    4

    Returns: 1625

  43. {-1,-1,2}

    {1,-1,-1}

    4

    Returns: 12900

  44. {1,2,-2}

    {3,1,-1}

    4

    Returns: 13715

  45. {3,3,0}

    {0,2,2}

    4

    Returns: 15295

  46. {0,-2,-2}

    {-3,-1,1}

    4

    Returns: 17372

  47. {-2,-2,-2,-3,-3,-3,-2}

    {1,0,-1,-2,-3,0,-2}

    4

    Returns: 0

  48. {-2,-2,-1,0,0,-1,0}

    {0,-1,-1,0,1,1,-1}

    4

    Returns: 0

  49. {2,0,0,-2,0}

    {2,2,0,-1,-2}

    4

    Returns: 1296

  50. {1,1,1,1,1,1,2}

    {3,2,1,0,-1,-2,-1}

    4

    Returns: 1930

  51. {2,1,0,-1,-2}

    {2,1,0,-1,-2}

    4

    Returns: 2450

  52. {2,1,0,-1,-2}

    {0,0,0,0,0}

    4

    Returns: 2450

  53. {-3,-3,-3,-3,-2,-1,0,1,2,3,3,3,3,2,1,0,-2,-2,-1,0,1,1,2,1,0,-1,-2,-2,-1,-1,0,0,2,2,1}

    {0,-1,-2,-3,-3,-3,-3,-2,-1,0,1,2,3,3,3,3,0,1,1,1,2,1,0,-1,-2,-2,-2,-1,0,-1,0,-1,1,2,0}

    4

    Returns: 1

  54. {-2,-3,-3,-3,-3,-2,-2,-2,-1,-1,-1,-1,0,0,0,0,0,-1,-2,-1,0,0,1,1,1,1,1,1,2,2,2,2,3,3,3,3,2}

    {0,0,-1,-2,-3,-3,-2,-1,0,-1,-2,-3,-3,-2,-1,0,1,1,1,2,2,3,3,2,1,0,-1,-2,0,1,2,3,3,2,1,0,-1}

    4

    Returns: 1

  55. {-3}

    {-3}

    4

    Returns: 117600

  56. {-2,1,1,-2,3,3,-2,-3,1,1,-1,1,3,-1,-3,0,0,0,0,3,1,-2,-3,-3,2,-1,2,-1,0,0,-2,-1,2,2,2,-1,0}

    {1,0,-2,-3,2,0,0,-2,2,1,2,3,1,-2,-1,-1,0,3,1,3,-1,-1,0,-3,1,1,-1,-3,-2,-3,-2,0,2,3,0,-1,2}

    4

    Returns: 1

  57. {0,2,-2,1,0,-1,2,-2,1,1,0,-1,-2,2,1,0,0,-1,-1}

    {2,0,-1,1,0,-2,2,0,-1,0,1,-1,-2,1,2,-1,-2,0,1}

    3

    Returns: 1

  58. {0}

    {0}

    1

    Returns: 1

  59. {0,1,0,0,1,-1,-1}

    {0,0,-1,1,1,0,-1}

    2

    Returns: 1

    Here the entire battlefield is occupied by Petr's heroes. Therefore there exists only one possible arrangement.

  60. {0, 1, 0, 0, 1, -1, -1 }

    {0, 0, -1, 1, 1, 0, -1 }

    2

    Returns: 1

  61. {-1, 0, 0, 1, 2 }

    {0, 0, 1, 0, 0 }

    4

    Returns: 3180

  62. {0 }

    {0 }

    4

    Returns: 78408

  63. {0 }

    {0 }

    3

    Returns: 104

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: