Problem Statement
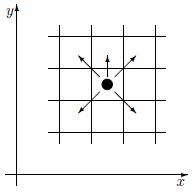
Initially, there's a Silver piece in cell (sx,sy) of an infinitely large board. Return the minimal number of steps required to move to cell (gx,gy).
Definition
- Class:
- SilverDistance
- Method:
- minSteps
- Parameters:
- int, int, int, int
- Returns:
- int
- Method signature:
- int minSteps(int sx, int sy, int gx, int gy)
- (be sure your method is public)
Constraints
- sx, sy, gx and gy will each be between -1,000,000 and 1,000,000 inclusive.
Examples
1
0
1
9
Returns: 9
Move up vertically in the positive y direction 9 times.
0
0
-4
3
Returns: 5
Follow the path : (0,0) -> (-1,1) -> (-1,2) -> (-2,3) -> (-3,2) -> (-4,3)
0
0
5
8
Returns: 8
Move up vertically in the postive y direction 3 times, then move diagonally up and to the right 5 times.
-487617
826524
892309
-918045
Returns: 1744571
-27857
31475
-27857
31475
Returns: 0
The Silver is already in the goal.
765193
377201
765191
377199
Returns: 2
-784373
390934
-784375
390933
Returns: 3
-330706
475232
-330708
475232
Returns: 2
349530
-113416
349528
-113415
Returns: 3
-583109
-842787
-583111
-842785
Returns: 2
699638
-732089
699637
-732091
Returns: 4
771899
-921638
771898
-921639
Returns: 1
753056
-453698
753055
-453698
Returns: 2
117356
-862744
117355
-862743
Returns: 1
931180
957388
931179
957390
Returns: 2
225981
669490
225981
669488
Returns: 2
-62771
-967730
-62771
-967731
Returns: 3
206592
-293811
206592
-293811
Returns: 0
637628
-432514
637628
-432513
Returns: 1
487223
-224313
487223
-224311
Returns: 2
-873913
949777
-873912
949775
Returns: 4
-484806
-458089
-484805
-458090
Returns: 1
40211
604450
40212
604450
Returns: 2
-572756
-281687
-572755
-281686
Returns: 1
-731157
998155
-731156
998157
Returns: 2
-63277
642461
-63275
642459
Returns: 2
914348
266372
914350
266371
Returns: 3
350865
-249640
350867
-249640
Returns: 2
-420991
-440652
-420989
-440651
Returns: 3
-500280
-30094
-500278
-30092
Returns: 2
-732513
-542725
58853
-776738
Returns: 791367
-571559
252635
-156169
-159253
Returns: 415390
674079
934097
686838
-858508
Returns: 1792605
-330110
230031
964597
-370703
Returns: 1294708
-46250
-598134
-469307
35292
Returns: 633426
653128
-124996
337064
-873188
Returns: 748192
565990
-966563
656244
-570391
Returns: 396172
653164
287035
218540
91958
Returns: 434625
98554
-419937
221228
622379
Returns: 1042316
-574481
579426
442096
426106
Returns: 1016578
-20853
170601
638444
-783689
Returns: 954292
636591
227526
-113385
160718
Returns: 749976
839931
-701149
81406
-904628
Returns: 758525
758207
205845
400672
486463
Returns: 357536
885971
-715746
-117854
833476
Returns: 1549222
170184
784167
999772
-17176
Returns: 829589
-539857
748436
-896740
12797
Returns: 735639
168858
569210
997844
997385
Returns: 828987
670859
-973579
323107
-590101
Returns: 383478
-1000000
-1000000
1000000
1000000
Returns: 2000000
-1000000
-1000000
1000000
999999
Returns: 2000001
-1000000
-1000000
999999
1000000
Returns: 2000000
1000000
1000000
-1000000
-1000000
Returns: 2000000
1000000
1000000
-1000000
-999999
Returns: 2000001
1000000
1000000
-999999
-1000000
Returns: 2000002
1000000
-1000000
-1000000
1000000
Returns: 2000000
-1000000
1000000
1000000
-999999
Returns: 2000001
-1000000
1000000
999999
-1000000
Returns: 2000002
1000000
-1000000
-1000000
1000000
Returns: 2000000
1000000
-1000000
-999999
1000000
Returns: 2000000
1000000
-1000000
-1000000
999999
Returns: 2000001
0
0
1
-4
Returns: 6
0
1
0
-1
Returns: 2
0
0
8
0
Returns: 8
1
10
11
10
Returns: 10
0
0
1
0
Returns: 2
800000
800000
500000
600000
Returns: 300000
999999
999999
-999999
-999999
Returns: 1999998
0
0
0
-1
Returns: 3
0
0
-3
-1
Returns: 3
0
0
1
-1
Returns: 1
-1000000
-1000000
1000000
999001
Returns: 2000001
5
10
5
9
Returns: 3
-48761
82654
892309
-918045
Returns: 1000701
0
0
10
-10
Returns: 10
1000000
1000000
-999999
0
Returns: 2000000
-999999
999999
999999
999998
Returns: 1999999
1
1
-9
1
Returns: 10
0
0
3
0
Returns: 4
-900000
-500000
1000000
700000
Returns: 1900000
-999999
-999997
999999
999104
Returns: 1999999
0
0
10001
-3
Returns: 10001
0
0
300
-1
Returns: 301
-478617
826582
896365
-914745
Returns: 1741329
0
0
2
1
Returns: 3
0
0
0
-2
Returns: 2
4
1
1
4
Returns: 3
0
0
3
3
Returns: 3
-1000000
-1000000
999999
666666
Returns: 2000000
0
1
3
1
Returns: 4
987654
989898
-998877
-897976
Returns: 1986532
0
0
1
-3
Returns: 3
-643039
155704
-426405
83934
Returns: 216634
10
2
4
2
Returns: 6
0
0
1
-2
Returns: 4
-99999
123
-999991
99998
Returns: 899993
0
0
2
-1
Returns: 3
0
0
5
-8
Returns: 10
-483649
640827
201850
-510648
Returns: 1151475
0
0
4
-3
Returns: 5
10
10
20
30
Returns: 20
0
1
3
0
Returns: 3
2
0
0
0
Returns: 2
100
1
0
0
Returns: 101
0
2
0
-3
Returns: 7
999999
0
0
0
Returns: 1000000
0
0
0
-5
Returns: 7
0
1
0
0
Returns: 3
12345
-12345
12245
-12444
Returns: 101
0
0
-30
-27
Returns: 31
-1000000
-1000000
999991
-892344
Returns: 1999992
-16563
-15432
875581
509110
Returns: 892144
100
101
-100000
-99999
Returns: 100100
-487617
826524
892309
-918049
Returns: 1744575
0
0
19233
9382
Returns: 19234
-1000000
1000000
999997
-1000000
Returns: 2000002
0
0
-1
-2
Returns: 4
960864
17412
-825303
-522786
Returns: 1786168
0
0
4
2
Returns: 4
-1000000
-1000000
999999
999998
Returns: 2000000
0
0
8
-5
Returns: 9
0
0
10
-20
Returns: 20
23422
23423
-23423
-23492
Returns: 46915
0
0
5
2
Returns: 6
0
0
2
0
Returns: 2
0
0
-1
-4
Returns: 6
2
3
0
0
Returns: 5
0
0
-2
0
Returns: 2
28703
31322
23811
30333
Returns: 4893
100
0
0
0
Returns: 100
368690
-479941
-102237
513926
Returns: 993867
-999998
1
999998
-1
Returns: 1999996
5
5
8
4
Returns: 3
0
0
7
0
Returns: 8
0
0
30
-31
Returns: 33
-99999
-99998
99999
99999
Returns: 199999
0
0
3
1
Returns: 3
0
0
1
1
Returns: 1
1
1
0
0
Returns: 1
0
2
0
0
Returns: 2
1
1
5
3
Returns: 4
0
-3
0
-5
Returns: 2
0
0
-4
-1
Returns: 5