Statistics

Problem Statement

Cat Taro likes dice. He has a die which is a 1 x 1 x 1 cube where each face contains a number between 1 and 6. Each number appears on exactly one face, and the sum of the numbers on opposite faces is always 7.

There is an infinitely large board which is divided into 1 x 1 cells. The board has a coordinate system in which the x-coordinate (the first coordinate) increases from left to right, while the y-coordinate (the second coordinate) increases from bottom to top. Taro initially places the die on the cell with coordinates (0, 0). The die shows '1' on the top face, '2' on the front face, and '3' on the left face (so the bottom face shows '6', the back face shows '5', and the right face shows '4').

Taro wants to move this die to cell (goalx, goaly) by performing a sequence of rotations. There are two ways to rotate the die:

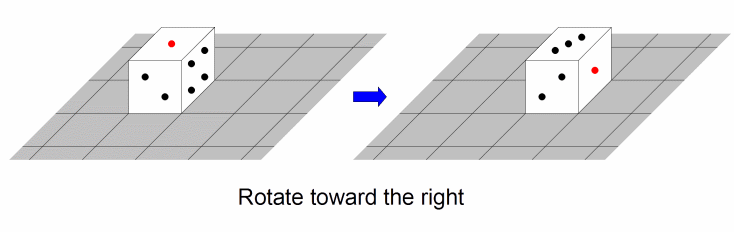
• Rotate toward the right. This operation moves the die from cell (x, y) to cell (x+1, y).
• Rotate toward the top. This operation moves the die from cell (x, y) to cell (x, y+1).

For example, if Taro's first rotation is toward the right, then the die will move to cell (1, 0) and the top face will show '3'.



Return the number of sequences of rotations which move the die to cell (goalx, goaly), such that the following conditions are satisfied:

• The die must show '1' again on the top face when it reaches (goalx, goaly).
• The die must not show '1' on the top face before it reaches (goalx, goaly).

Definition

Class:

DiceRotation

Method:

theCount

Parameters:

int, int

Returns:

int

Method signature:

int theCount(int goalx, int goaly)

(be sure your method is public)

Notes

• The answer will always fit in a signed 32-bit integer.

Constraints

• goalx will be between 1 and 1,000,000,000, inclusive.
• goaly will be between 1 and 1,000,000,000, inclusive.

Examples

1. 2

   2

   Returns: 2

   There are two ways to move the die to cell (2,2) that satisfy the conditions: right -> right -> up -> up up -> up -> right -> right

2. 5

   8

   Returns: 2

3. 47

   58

   Returns: 2

4. 489

   489

   Returns: 2

5. 1000000000

   1000000000

   Returns: 2

6. 4

   4

   Returns: 12

7. 4

   1000000000

   Returns: 1000000003

8. 1

   1

   Returns: 0

9. 1

   2

   Returns: 0

10. 1

    3

    Returns: 0

11. 1

    4

    Returns: 2

12. 2

    1

    Returns: 0

13. 2

    3

    Returns: 2

14. 2

    4

    Returns: 5

15. 3

    1

    Returns: 0

16. 3

    2

    Returns: 2

17. 3

    3

    Returns: 2

18. 3

    4

    Returns: 6

19. 4

    1

    Returns: 2

20. 4

    2

    Returns: 5

21. 4

    3

    Returns: 6

22. 1

    1000000000

    Returns: 0

23. 2

    1000000000

    Returns: 2

24. 3

    1000000000

    Returns: 2

25. 4

    1000000000

    Returns: 1000000003

26. 5

    1000000000

    Returns: 2

27. 1

    21861532

    Returns: 0

28. 1

    84

    Returns: 0

29. 8690127

    1

    Returns: 0

30. 14672330

    1

    Returns: 0

31. 2

    15883626

    Returns: 2

32. 2

    1386936

    Returns: 2

33. 1087700

    2

    Returns: 2

34. 45049380

    2

    Returns: 2

35. 3

    31

    Returns: 2

36. 3

    72

    Returns: 2

37. 88497419

    3

    Returns: 2

38. 171051902

    3

    Returns: 2

39. 4

    280080348

    Returns: 280080351

40. 4

    2050964

    Returns: 2050967

41. 20032

    4

    Returns: 20035

42. 2916

    4

    Returns: 2919

43. 933890

    4

    Returns: 933893

44. 4791339

    4

    Returns: 4791342

45. 5

    1

    Returns: 0

46. 5

    2

    Returns: 2

47. 5

    3

    Returns: 2

48. 5

    4

    Returns: 8

49. 5

    5

    Returns: 2

50. 21861532

    84

    Returns: 2

51. 8690127

    14672330

    Returns: 2

52. 15883626

    1386936

    Returns: 2

53. 1087700

    45049380

    Returns: 2

54. 31

    72

    Returns: 2

55. 88497419

    171051902

    Returns: 2

56. 20032

    2916

    Returns: 2

57. 933890

    4791339

    Returns: 2

58. 119187

    26

    Returns: 2

59. 112984

    1392043

    Returns: 2

60. 280

    941150

    Returns: 2

61. 25390

    146711

    Returns: 2

62. 4

    2247417

    Returns: 2247420

63. 1000000000

    4

    Returns: 1000000003

64. 4

    25

    Returns: 28

65. 100000

    4

    Returns: 100003

66. 4

    10000

    Returns: 10003

67. 4

    5

    Returns: 8

68. 1000000

    4

    Returns: 1000003

69. 100

    4

    Returns: 103

70. 4

    1000000

    Returns: 1000003

71. 4

    10

    Returns: 13

72. 4

    7

    Returns: 10

73. 99999

    4

    Returns: 100002

74. 100000000

    100000000

    Returns: 2

75. 1

    100

    Returns: 0

76. 4

    1000

    Returns: 1003

77. 4

    50

    Returns: 53

78. 4

    16

    Returns: 19

79. 1000

    4

    Returns: 1003

80. 4

    9999

    Returns: 10002

81. 4

    49

    Returns: 52

82. 4

    100

    Returns: 103

83. 4

    230

    Returns: 233

84. 1

    1000

    Returns: 0

85. 1

    80000

    Returns: 0

86. 123

    4

    Returns: 126

87. 1

    10

    Returns: 0

88. 4

    400

    Returns: 403