Problem Statement
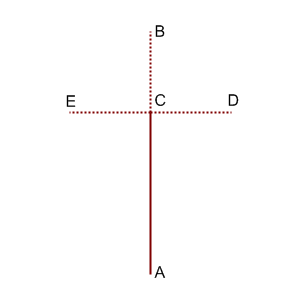
Each generation of the fractal can be described as a set of segments on the plane. Some of these segments are called final and all other are considered to be non-final. In each non-final segment, one of its endpoints is chosen and called the root of this segment. In pictures below, solid and dotted lines are used to represent final and non-final segments, correspondingly.
The first generation consists of one segment with endpoints (0, 0) and (0, 81). This segment is non-final and its root is (0, 0).

The i-th generation, i >= 2, is produced from the (i-1)-th generation as follows. All final segments from the (i-1)-th generation are included into the i-th generation without any changes. For each non-final segment from the (i-1)-th generation, let A and B be its endpoints, with A being its root. The following steps are then done:
- The point C is drawn on the segment AB so that the length of segment AC is twice as large as the length of segment BC.
- Segment CD is drawn as the rotation of segment CB around point C by 90 degrees clockwise.
- Segment CE is drawn as the rotation of segment CB around point C by 90 degress counter-clockwise.
- Segment AC is included in the i-th generation as a final segment.
- Segments CB, CD and CE are included in the i-th generation as non-final segments. The root of each of these three segments is point C.

Consider a rectangle R on the plane that consists of points (x, y), such that x1 <= x <= x2 and y1 <= y <= y2. Let S be the set of all segments of the 500-th generation of the fractal described above (both final and non-final ones). Return the total length of all parts of segments from S that belong to rectangle R.
Definition
- Class:
- FractalPicture
- Method:
- getLength
- Parameters:
- int, int, int, int
- Returns:
- double
- Method signature:
- double getLength(int x1, int y1, int x2, int y2)
- (be sure your method is public)
Notes
- The returned value must have an absolute or relative error less than 1e-9.
Constraints
- x1 will be between -100 and 100, inclusive.
- x2 will be between x1+1 and 100, inclusive.
- y1 will be between -100 and 100, inclusive.
- y2 will be between y1+1 and 100, inclusive.
Examples
-1
0
1
53
Returns: 53.0
Only one part of fractal segments belongs to this rectangle: (0, 0) - (0, 53).
1
1
10
10
Returns: 0.0
No parts of fractal segments belong to this rectangle.
-10
54
10
55
Returns: 21.0
Two parts of fractal segments belong to this rectangle: (-10, 54) - (10, 54) and (0, 54) - (0, 55). Note that parts that lie on the rectangle's border also belong to the rectangle.
14
45
22
54
Returns: 2999.0
0
80
1
81
Returns: 332.0
-100
-100
100
100
Returns: 27027.0
-28
44
-16
62
Returns: 6992.0
-28
44
-16
63
Returns: 7653.0
-28
44
-16
64
Returns: 7653.0
-28
44
-15
62
Returns: 8315.0
-28
44
-15
63
Returns: 8976.0
-28
44
-15
64
Returns: 8976.0
-28
44
-14
62
Returns: 8316.0
-28
44
-14
63
Returns: 8977.0
-28
44
-14
64
Returns: 8977.0
-28
45
-16
62
Returns: 6992.0
-28
45
-16
63
Returns: 7653.0
-28
45
-16
64
Returns: 7653.0
-28
45
-15
62
Returns: 8315.0
-28
45
-15
63
Returns: 8976.0
-28
45
-15
64
Returns: 8976.0
-28
45
-14
62
Returns: 8316.0
-28
45
-14
63
Returns: 8977.0
-28
45
-14
64
Returns: 8977.0
-28
46
-16
62
Returns: 6331.0
-28
46
-16
63
Returns: 6992.0
-28
46
-16
64
Returns: 6992.0
-28
46
-15
62
Returns: 7654.0
-28
46
-15
63
Returns: 8315.0
-28
46
-15
64
Returns: 8315.0
-28
46
-14
62
Returns: 7655.0
-28
46
-14
63
Returns: 8316.0
-28
46
-14
64
Returns: 8316.0
-27
44
-16
62
Returns: 6992.0
-27
44
-16
63
Returns: 7653.0
-27
44
-16
64
Returns: 7653.0
-27
44
-15
62
Returns: 8315.0
-27
44
-15
63
Returns: 8976.0
-27
44
-15
64
Returns: 8976.0
-27
44
-14
62
Returns: 8316.0
-27
44
-14
63
Returns: 8977.0
-27
44
-14
64
Returns: 8977.0
-27
45
-16
62
Returns: 6992.0
-27
45
-16
63
Returns: 7653.0
-27
45
-16
64
Returns: 7653.0
-27
45
-15
62
Returns: 8315.0
-27
45
-15
63
Returns: 8976.0
-27
45
-15
64
Returns: 8976.0
-27
45
-14
62
Returns: 8316.0
-27
45
-14
63
Returns: 8977.0
-27
45
-14
64
Returns: 8977.0
-27
46
-16
62
Returns: 6331.0
-27
46
-16
63
Returns: 6992.0
-27
46
-16
64
Returns: 6992.0
-27
46
-15
62
Returns: 7654.0
-27
46
-15
63
Returns: 8315.0
-27
46
-15
64
Returns: 8315.0
-27
46
-14
62
Returns: 7655.0
-27
46
-14
63
Returns: 8316.0
-27
46
-14
64
Returns: 8316.0
-26
44
-16
62
Returns: 6331.0
-26
44
-16
63
Returns: 6992.0
-26
44
-16
64
Returns: 6992.0
-26
44
-15
62
Returns: 7654.0
-26
44
-15
63
Returns: 8315.0
-26
44
-15
64
Returns: 8315.0
-26
44
-14
62
Returns: 7655.0
-26
44
-14
63
Returns: 8316.0
-26
44
-14
64
Returns: 8316.0
-26
45
-16
62
Returns: 6331.0
-26
45
-16
63
Returns: 6992.0
-26
45
-16
64
Returns: 6992.0
-26
45
-15
62
Returns: 7654.0
-26
45
-15
63
Returns: 8315.0
-26
45
-15
64
Returns: 8315.0
-26
45
-14
62
Returns: 7655.0
-26
45
-14
63
Returns: 8316.0
-26
45
-14
64
Returns: 8316.0
-26
46
-16
62
Returns: 5670.0
-26
46
-16
63
Returns: 6331.0
-26
46
-16
64
Returns: 6331.0
-26
46
-15
62
Returns: 6993.0
-26
46
-15
63
Returns: 7654.0
-26
46
-15
64
Returns: 7654.0
-26
46
-14
62
Returns: 6994.0
-26
46
-14
63
Returns: 7655.0
-26
46
-14
64
Returns: 7655.0
18
48
19
49
Returns: 2.0
19
44
21
49
Returns: 994.0
15
48
16
49
Returns: 332.0
19
45
21
47
Returns: 0.0
16
46
19
47
Returns: 333.0
19
47
21
48
Returns: 498.0
21
46
22
49
Returns: 0.0
15
47
17
49
Returns: 994.0
18
45
21
49
Returns: 1495.0
19
62
23
69
Returns: 0.0
17
53
25
63
Returns: 3002.0
19
59
21
61
Returns: 994.0
17
50
25
61
Returns: 3005.0
19
57
26
65
Returns: 994.0
21
56
24
62
Returns: 332.0
23
48
25
52
Returns: 663.0
20
48
27
49
Returns: 332.0
-13
52
9
69
Returns: 39.0
0
44
8
54
Returns: 18.0
2
62
20
65
Returns: 663.0
-1
48
23
69
Returns: 4040.0
3
67
14
68
Returns: 0.0
11
55
16
67
Returns: 663.0
12
50
25
59
Returns: 2012.0
6
47
11
49
Returns: 0.0
8
48
9
58
Returns: 1.0
-15
45
-8
67
Returns: 7.0
0
71
7
79
Returns: 2006.0
-3
71
1
81
Returns: 2002.0
-2
72
1
74
Returns: 5.0
-9
72
4
81
Returns: 4495.0
0
70
4
81
Returns: 1506.0
-3
70
9
72
Returns: 844.0
-6
77
6
81
Returns: 2986.0
-65
-13
28
24
Returns: 24.0
-79
-59
-49
-42
Returns: 0.0
-71
-60
-17
85
Returns: 6986.0
2
28
66
74
Returns: 11317.0
-16
-88
63
71
Returns: 12392.0
11
-60
90
-47
Returns: 0.0
70
-34
100
-13
Returns: 0.0
-81
-63
-35
10
Returns: 0.0
-91
19
72
26
Returns: 7.0
-33
-61
85
0
Returns: 0.0
-25
60
-5
75
Returns: 4979.0
-25
60
5
85
Returns: 7992.0
-25
60
5
65
Returns: 1998.0
-5
60
5
65
Returns: 5.0
-5
50
5
65
Returns: 25.0
-5
-50
5
65
Returns: 75.0
-5
-50
5
5
Returns: 5.0
0
-50
5
65
Returns: 70.0
0
50
1
65
Returns: 16.0
-1
50
0
65
Returns: 16.0
0
54
10
72
Returns: 1528.0
0
54
100
72
Returns: 6027.0
-100
54
0
78
Returns: 8023.0
-100
54
-1
78
Returns: 7996.0
-100
55
18
80
Returns: 13812.0
-100
55
18
81
Returns: 14473.0
26
54
27
55
Returns: 332.0
26
53
27
54
Returns: 332.0
26
53
27
55
Returns: 663.0
18
55
20
56
Returns: 1.0
19
55
20
56
Returns: 0.0
-19
17
24
59
Returns: 6081.0
14
45
32
54
Returns: 4495.0
-27
53
-26
55
Returns: 663.0
-25
25
55
77
Returns: 23022.0
-1
57
1
58
Returns: 1.0
-28
55
2
99
Returns: 9324.0