Statistics

Problem Statement for "CaptureFish"

Problem Statement

There are N fish and N+1 buoys in a small pond. Mr. Jeipouju wants to capture some of the fish.

In this problem, regard the pond as a 2-dimensional Cartesian plane (as seen from above). Each fish and each buoy is a point on the plane. The buoys are lined up on x axis and numbered 0 to N from left to right. There is exactly one fish between each two neighboring buoys. The fish are numbered 0 to N-1 from left to right. For the purpose of this problem we will assume that the fish are staying on their spots without any movement. The exact coordinates of the fish and the buoys do not matter. See the following image for clarity.

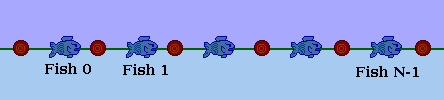You are given a String fish with N characters. Each character of fish is either letter 'O' or 'X' or '*'. If fish[i] is 'O', it represents that he must capture fish i. If fish[i] is 'X', he must not capture fish i. If fish[i] is '*', he does not care whether he capture fish i or not.

To capture the fish, Mr. Jeipouju wants to set up a net in the pond so that the net will separate the caught fishes from the uncaught ones. From above, the net must be a closed curve in our plane. Furthermore, this closed curve must satisfy the following conditions:

  • The net is not allowed to pass through any of the fish.
  • The net is not allowed to touch or intersect itself.
  • The net may only cross the x axis at points that contain the buoys. The net is not allowed to touch the x axis without crossing it.
  • The net must cross the x axis at least twice.
  • The fish Mr. Jeipouju wants to capture and the fish he wants not to capture must be separated by the net. That is, either all fish marked with 'X' are to be inside the net and all fish marked with 'O' outside, or vice versa. The fish marked '*' may be anywhere, possibly some of them inside and some outside the net.
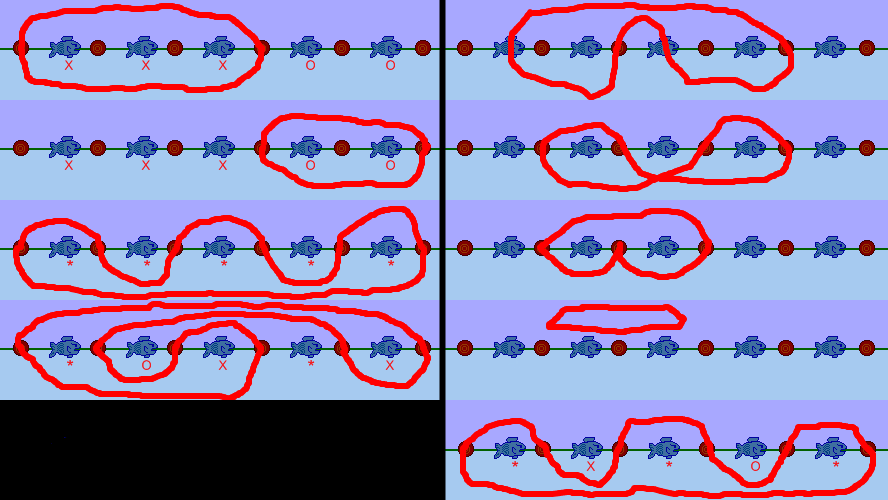The following image shows some examples of valid and invalid net placements: 4 nets to the left are valid and 5 nets to the right are invalid.

A net can be encoded into a sequence using the following algorithm:

  • Start anywhere on the net, but not on a buoy.
  • Walk along the net until you reach your starting point again.
  • During the walk, each time you encounter a buoy, write down its number and the halfplane in which you are moving away from the x axis. (The halfplane is "+" if after visiting the buoy your y coordinate is positive and "-" if it is negative.)
In this way you will obtain some sequence (buoy1,side1,...,buoyK,sideK). Two nets are considered the same if they can be encoded to the same sequence.

Mr. Jeipouju wants to know whether the number of different nets is odd or even. Your method must return the number of different nets, modulo 2.

Definition

Class:
CaptureFish
Method:
getParity
Parameters:
String
Returns:
int
Method signature:
int getParity(String fish)
(be sure your method is public)

Constraints

  • fish will contain between 1 and 50 characters, inclusive.
  • Each character of fish will be either letter 'O' or 'X' or '*'.
  • fish will contain at least one 'O' character.

Examples

  1. "OXOXO"

    Returns: 0

    In this case, there are 5 fish. There are 8 ways to separate them.

  2. "OO"

    Returns: 1

    There is only one valid net and it looks as follows: Two things to notice: First, the net does not have to pass through all the buoys. Second, it is allowed to have no fish at all at either side of the net.

  3. "**OX**"

    Returns: 0

  4. "O***O***O***O"

    Returns: 1

  5. "O*X**X***X*O"

    Returns: 0

  6. "O"

    Returns: 1

  7. "OX"

    Returns: 0

  8. "XO"

    Returns: 0

  9. "*O"

    Returns: 1

  10. "O*"

    Returns: 1

  11. "O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O"

    Returns: 1

  12. "X*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*O*X"

    Returns: 0

  13. "OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO"

    Returns: 1

  14. "OXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"

    Returns: 0

  15. "***********************************************O**"

    Returns: 1

  16. "*************O************************************"

    Returns: 1

  17. "O************************************************O"

    Returns: 1

  18. "O***********************X************************O"

    Returns: 0

  19. "O**********************X************************O"

    Returns: 1

  20. "O*********************X************************O"

    Returns: 0

  21. "XOOXOXXOOO"

    Returns: 0

  22. "XOXXXXOXXOXXOXX"

    Returns: 0

  23. "OXOXXOOXXXXXXOXXOOXX"

    Returns: 0

  24. "OOOXXOXOOOOXOXOXXXOOOXOOO"

    Returns: 0

  25. "OOOXXXXOOXXXOOOXOXOXOOXXOOXXOO"

    Returns: 0

  26. "XOOXXXXOXXXXOXXXOXOXOOXOOOOOXXXOOOX"

    Returns: 0

  27. "***OXX*X*"

    Returns: 0

  28. "XO*OOO*XO*O*XXXX*"

    Returns: 0

  29. "XX*X*OXXXXXO*XOXOXXXOOX*X"

    Returns: 0

  30. "*O*XX*XO**XXXXXOXXOX*X********OOX"

    Returns: 0

  31. "*OXXO**X**OX*X*O**X*XXOX*X*XX**X*XX*XO**X"

    Returns: 0

  32. "XX**OOXX**OO*O*XXO*XOXXXXOXXO*X*XXX*OX**X*XXXX*OX"

    Returns: 0

  33. "*X*OXX*O*O"

    Returns: 0

  34. "**O*OX***OXXO**O*X"

    Returns: 0

  35. "*XOXX*X****XX*O***XO***OOX"

    Returns: 0

  36. "*XOOOXOO***O**XOX*X*OOO**OOO***O**"

    Returns: 0

  37. "*OO*O**O**X***OXOOOO*O***OX*OOX**O*X*XOO*O"

    Returns: 0

  38. "O***OOOXX**XOXOOO***OX****OXOX*OXO*XXOO***XOO*XO*O"

    Returns: 0

  39. "****XXO**X********O**OO**X****"

    Returns: 0

  40. "O*X***X*O***************X*****X*O"

    Returns: 0

  41. "O***O**X*****OX**OXO****O*********X*"

    Returns: 0

  42. "*********X**X********O*****X******O**X*"

    Returns: 0

  43. "**OO**XX******O**********O****X**OX***X*XX"

    Returns: 0

  44. "*X***********X**OX*X**O******O*O********X****"

    Returns: 0

  45. "******O***"

    Returns: 1

  46. "**O****O*O**O**OOO"

    Returns: 1

  47. "O*O**O**O*****O*OOO*****O*"

    Returns: 1

  48. "**O*****O*O**O*O*OO****O*OO******O"

    Returns: 1

  49. "**O**O******O*OO*OOOO***O*O*OO****O***OOO*"

    Returns: 0

  50. "OO**OO*OOOOOOOOOO*OOO*O**OOO****OOO*O*OOO*OO***OO*"

    Returns: 1

  51. "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXOOOOOXXXXXXXXXXXXXXX"

    Returns: 1

  52. "XXXXXXXXXXXXXXXXXXXXXOOOOOOOOOOOOOOOOOOOOOOOOOOXXX"

    Returns: 1

  53. "OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOXXXXXXXXXX"

    Returns: 0

  54. "OOOOOOOOOOOOOXXXXXXXXXXXXXXXXOOOOOOOOOOOOOOOOOOOOO"

    Returns: 1

  55. "OOOOOOOOOOOOOOOOOOOOXXXXXXXXXXXXXXXXXXXXXXXXXXXXOO"

    Returns: 1

  56. "XXXXXXXXOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOXXX"

    Returns: 1

  57. "*O*O*OOO**OO**O*******X**X*XOO*O***OOOO*******OO*O"

    Returns: 0

  58. "XXXXX*XX*XX***XX*X*X*XXX*XXOOOOO*XXX*XXXXX*XX*XXX"

    Returns: 0

  59. "O**O**OOOOO*O*XXXXXXXX*XXXX**XXXXX**XXXXXXXXOOO*"

    Returns: 0

  60. "XX*XXXXXXXX*XXXXOOOOOXX**XXXXX*XXXXXXX*X***XXX*"

    Returns: 1

  61. "*OOXXXXXXX*XXX*XXXX*XXX*X***X*X***O*OOO*OOOO*O"

    Returns: 0

  62. "*OO*O*XX*XX**XXX**XX*XX**XOOO*OO*O*OOOOO**O*O"

    Returns: 0

  63. "*X**XX**X*X*******O*OO**OO**********X*************"

    Returns: 0

  64. "*XX**XX**XX*XX****OOO*****O***O********X**********"

    Returns: 1

  65. "*******O****O*****XX******X***X*X*X***OOO****OOO**"

    Returns: 0

  66. "OO***O***O*******X****X*******X*X*********O****O**"

    Returns: 0

  67. "***********O******X***X*****X***X**XOO*O****O*O*O*"

    Returns: 1

  68. "**O***OO****OOO************XX**X*X**O*****OO******"

    Returns: 1

  69. "O*O***O**O**O*OO****OOO*O**O**O*O*****X*XXX*XX****"

    Returns: 0

  70. "**O***O*O*****OO******O*O***OOO*OO**X**X****XXXX**"

    Returns: 0

  71. "***OOO***O*****OO*OOO*OO**OOO*OOO**X*X*****X***X**"

    Returns: 1

  72. "O*O******OO******OOOOO*****OO**********XX**X**X***"

    Returns: 1

  73. "***XX**XX*X**XXXXXXX*XX*XX*XXXX*XXOO**O*****O*OOO*"

    Returns: 0

  74. "X*********XXXX*XX**XX****X***XX*X*OOO****OOO*O***O"

    Returns: 0

  75. "OXOXOXOOO"

    Returns: 0

  76. "OX*"

    Returns: 1

  77. "*O*O**"

    Returns: 1

  78. "XOX"

    Returns: 1

  79. "OOOX*"

    Returns: 1

  80. "OOOOOOO"

    Returns: 1

  81. "OXO"

    Returns: 1

  82. "*OX"

    Returns: 1

  83. "X*OX"

    Returns: 0

  84. "OXXO"

    Returns: 1

  85. "XOOX"

    Returns: 1

  86. "O*O"

    Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: