Statistics

Problem Statement

This problem contains images

Elwood has a little sister named Casey. Although being quite young, Casey not only likes Modern Art, but also creates little pieces of art by herself. Her latest favorites are drawings on squared paper. She wants her new creations to be composed of only one basic shape that is used in all orientations:

[Image showing Casey's basic shape in all orientations.]

She draws her shapes into rectangles on her paper. For a rectangle of a given size, she wants to fill the entire rectangle in all different ways. Elwood immediately recognizes that even for small rectangles there might be many different fillings. But Casey, like little sisters sometimes do, doesn't believe him, so she asks you to exactly calculate how many drawings she has to do for a rectangle of a given size.

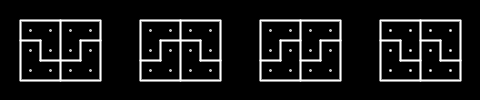
[Image showing all four possible fillings of a 3x4 rectangle.]

Given an int length and an int width describing the size of Casey's rectangle, return the number of different ways this rectangle can be filled using Casey's basic shape. The rectangle is oriented, so count symmetrical fillings multiple times as done in the example above.

Definition

Class:

CaseysArt

Method:

howManyWays

Parameters:

int, int

Returns:

double

Method signature:

double howManyWays(int length, int width)

(be sure your method is public)

Notes

• Reminder:If your result is within 10-9 of the expected result, your solution will be evaluated as correct.If your result is between (1+10-9)*expected and (1-10-9)*expected, it will be evaluated as correct.

Constraints

• length will be between 1 and 18, inclusive.
• width will be between 1 and 15, inclusive.

Examples

1. 3

   4

   Returns: 4.0

   This is the rectangle shown in the problem description.

2. 4

   3

   Returns: 4.0

   This is the rectangle shown in the problem description rotated.

3. 2

   2

   Returns: 0.0

   A rectangle of size 2x2 can't be filled.

4. 5

   9

   Returns: 384.0

5. 1

   1

   Returns: 0.0

6. 1

   2

   Returns: 0.0

7. 1

   3

   Returns: 0.0

8. 1

   12

   Returns: 0.0

9. 2

   3

   Returns: 2.0

10. 2

    4

    Returns: 0.0

11. 2

    9

    Returns: 8.0

12. 2

    12

    Returns: 16.0

13. 3

    2

    Returns: 2.0

14. 3

    12

    Returns: 64.0

15. 4

    12

    Returns: 468.0

16. 5

    8

    Returns: 0.0

17. 6

    2

    Returns: 4.0

18. 6

    6

    Returns: 162.0

19. 6

    11

    Returns: 39088.0

20. 7

    4

    Returns: 0.0

21. 7

    15

    Returns: 1.15363072E8

22. 8

    1

    Returns: 0.0

23. 8

    3

    Returns: 16.0

24. 8

    9

    Returns: 204184.0

25. 8

    12

    Returns: 2.9986082E7

26. 9

    2

    Returns: 8.0

27. 9

    3

    Returns: 0.0

28. 9

    9

    Returns: 1193600.0

29. 9

    11

    Returns: 6.3112256E7

30. 10

    9

    Returns: 9567192.0

31. 10

    11

    Returns: 0.0

32. 10

    12

    Returns: 7.75880967E9

33. 11

    9

    Returns: 6.3112256E7

34. 11

    11

    Returns: 0.0

35. 11

    12

    Returns: 1.24693887784E11

36. 12

    6

    Returns: 118586.0

37. 12

    12

    Returns: 2.033502499954E12

38. 13

    2

    Returns: 0.0

39. 13

    6

    Returns: 361712.0

40. 13

    9

    Returns: 3.245128576E9

41. 13

    12

    Returns: 3.3128240650256E13

42. 14

    3

    Returns: 128.0

43. 14

    5

    Returns: 0.0

44. 14

    6

    Returns: 1103946.0

45. 14

    9

    Returns: 2.3378489272E10

46. 14

    11

    Returns: 0.0

47. 14

    12

    Returns: 5.38556346650082E14

48. 15

    11

    Returns: 2.33712926959296E14

49. 15

    12

    Returns: 8.7786436827666E15

50. 15

    13

    Returns: 3.281779116794919E17

51. 15

    15

    Returns: 4.583240929968676E20

52. 16

    15

    Returns: 1.7126367065533525E22

53. 17

    13

    Returns: 0.0

54. 17

    15

    Returns: 6.401450746057415E23

55. 18

    6

    Returns: 1.0153017E8

56. 18

    9

    Returns: 5.9141914295736E13

57. 18

    12

    Returns: 3.79195817400869E19

58. 18

    13

    Returns: 3.252838833028188E21

59. 18

    14

    Returns: 2.7869302738761328E23

60. 18

    15

    Returns: 2.393036288950159E25

61. 18

    15

    Returns: 2.393036288950159E25

62. 3

    4

    Returns: 4.0

63. 5

    9

    Returns: 384.0

64. 15

    15

    Returns: 4.583240929968676E20

65. 6

    8

    Returns: 1514.0

66. 12

    12

    Returns: 2.033502499954E12

67. 4

    6

    Returns: 18.0

68. 9

    9

    Returns: 1193600.0

69. 13

    15

    Returns: 3.281779116794919E17