Problem Statement
This problem contains an image.
TopCan, Inc. is a major producer of food. It produces all kinds of food than can be filled into a can: pineapples, mushrooms, peas, etc. However, business is not going well, so they are looking for ways to make production cheaper. An important expense factor is the amount of material needed for producing the can, which directly depends on the surface area of the can. Currently, cans are produced in all imaginable shapes and sizes, but to reduce cost, the company thinks about producing only cans in the shape of a cylinder (as shown below). So to be able to decide whether production should be changed TopCan wants to know, for a given volume, the minimal surface area possible of such a can. As the company's brightest employee, this task has been assigned to you.
Given anint volume, return a double , the minimal surface area possible of a cylinder that has the given volume.
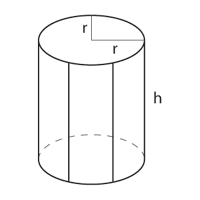
TopCan, Inc. is a major producer of food. It produces all kinds of food than can be filled into a can: pineapples, mushrooms, peas, etc. However, business is not going well, so they are looking for ways to make production cheaper. An important expense factor is the amount of material needed for producing the can, which directly depends on the surface area of the can. Currently, cans are produced in all imaginable shapes and sizes, but to reduce cost, the company thinks about producing only cans in the shape of a cylinder (as shown below). So to be able to decide whether production should be changed TopCan wants to know, for a given volume, the minimal surface area possible of such a can. As the company's brightest employee, this task has been assigned to you.
Given an

Definition
- Class:
- TopCan
- Method:
- minSurface
- Parameters:
- int
- Returns:
- double
- Method signature:
- double minSurface(int volume)
- (be sure your method is public)
Notes
- Consider the material the can is made of to be infinitely thin.
- Some formulas for your convenience:r: radius of the circle being the base of the cylinderh: height of the cylinderVolume V = h * PI * r2Surface S = 2 * PI * r * (r + h)
- If not provided by a library, use the value of 2*acos(0) for PI.
- Reminder:If your result is within 10-9 of the expected result, your solution will be evaluated as correct.If your result is between (1+10-9)*expected and (1-10-9)*expected, it will be evaluated as correct.
Constraints
- volume will be between 1 and 100000, inclusive.
Examples
10
Returns: 25.694955950835347
For a volume of 10, the cylinder has a height of about 2.3351 and the base circle has a radius of about 1.1675.
20
Returns: 40.78820010663257
1
Returns: 5.535810445932085
2
Returns: 8.787551325369138
3
Returns: 11.514949756065077
13
Returns: 30.606249366769717
117
Returns: 132.42554999383506
2048
Returns: 892.7595659593932
17280
Returns: 3700.07365692029
42376
Returns: 6728.648641647673
76294
Returns: 9958.061425281121
100000
Returns: 11926.542062156956
3
Returns: 11.514949756065077
26
Returns: 48.5843924416113
1
Returns: 5.535810445932085