Problem Statement
We have an infinite triangle grid. Onto that grid we have drawn a convex hexagon, as shown below.
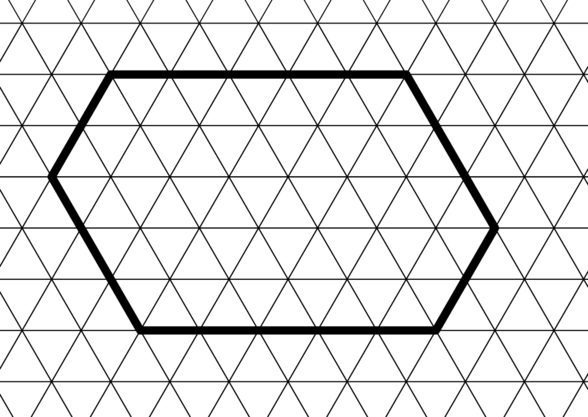
Note that opposite sides of the hexagon have the same length. Each such hexagon is determined by three numbers (A, B, C): A is the length of the horizontal side, B is the length of the side going "southeast", and C is the length of the edge going "southwest".
For example, the hexagon in the above figure is called a (5,3,2)-hexagon.
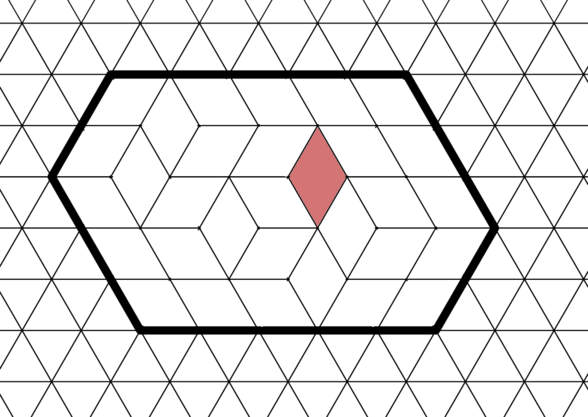
We are now going to tile the hexagon with diamonds. (Here, a diamond is a figure consisting of two unit triangles that share a side.)
The tiling must be perfect: each unit triangle inside the hexagon must be covered by exactly one diamond, and each diamond used in the tiling must be fully inside the hexagon. One such tiling is shown below.
In the tiling, one of the vertical diamonds is highlighted.
Consider all possible tilings of the given hexagon. For each of them, write down the number of vertical diamonds it contains. Return the sum of all the numbers you have written down, modulo 10^9 + 7.
Definition
- Class:
- HexagonTiled
- Method:
- count
- Parameters:
- int, int, int
- Returns:
- int
- Method signature:
- int count(int A, int B, int C)
- (be sure your method is public)
Constraints
- A will be between 1 and 50, inclusive.
- B will be between 1 and 50, inclusive.
- C will be between 1 and 50, inclusive.
Examples
1
1
1
Returns: 2
The smallest possible hexagon consists of six unit triangles only. It has two distinct tilings. Each tiling consists of three diamonds in different orientations, exactly one of them being vertical.
5
3
2
Returns: 7056
6
6
6
Returns: 298788286
2
2
2
Returns: 80
1
1
50
Returns: 2550
50
50
50
Returns: 681289496
50
47
49
Returns: 232573810
47
50
49
Returns: 609121077
47
49
50
Returns: 609121077
23
24
32
Returns: 120734249
27
3
49
Returns: 641565049
2
25
40
Returns: 820190433
10
50
10
Returns: 364173726