Statistics

Problem Statement for "ProbabilityTree"

Problem Statement

Probability trees are a useful tool in mathematics to help determine conditional probabilities of complex events. Each node in a probability tree represents an event. We write P(X) to mean "the probability that event X occurs", and P(~X) to mean "the probability that event X does not occur". If a node is at the root of the tree, it has a single number associated with it (between 0.0 and 1.0, inclusive) which represents the likelihood of this event taking place. All other nodes on the tree have two numbers attached to them: the probability of this event happening if the parent node's event occurs, and the probability of this event happening if the parent node's event does not occur. If the current node is A and the parent node is B, these probabilities are referred to as P(A|B) (probability of A given B) and P(A|~B) (probability of A given not-B), respectively.

For example, here is a tree with only two nodes:

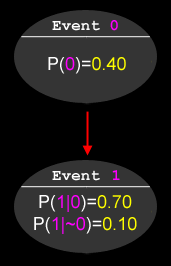
To calculate the probability of event 1 occurring (whether or not event 0 occurs), one can use this rule:
P(A) = P(A|B) * P(B) + P(A|~B) * P(~B)
The following diagram shows a more complete list of probabilities which can be derived:

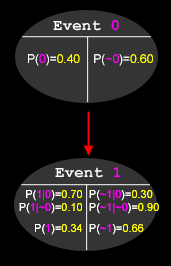
Note that the sum of two opposite events is always equal to 1. P(1) was calculated as follows:
P(1) = P(1|0) * P(0) + P(1|~0) * P(~0) = (0.4 * 0.7) + (0.6 * 0.1) = 0.34

You will be given a String[] tree, representing a probability tree. The first element of tree represents the root node, and will be a single integer between 1 and 99, inclusive, representing the percent likelihood of the event taking place. Each successive element of tree will be of the form "<parent> <prob1> <prob2>", where <parent> is the zero-based index of the parent node in tree, and <prob1> and <prob2> are P(A|B) and P(A|~B) for this node, respectively. You will also be given two percentages, lowerBound and upperBound. Your method should return a int[] containing every node X, in ascending order, such that lowerBound < P(X) < upperBound.

Definition

Class:
ProbabilityTree
Method:
getOdds
Parameters:
String[], int, int
Returns:
int[]
Method signature:
int[] getOdds(String[] tree, int lowerBound, int upperBound)
(be sure your method is public)

Constraints

  • tree will contain between 1 and 50 elements, inclusive.
  • Each element of tree will contain between 1 and 8 characters, inclusive.
  • The first element of tree will contain a single integer between 1 and 99, inclusive, with no leading zeroes.
  • All other elements of tree will contain three space-separated integers of the form " ", with no unnecessary leading zeroes.
  • will be an integer between 0 and N-1, inclusive, where N is the number of elements in tree.
  • and will be between 1 and 99, inclusive.
  • All nodes in tree will be connected, directly or indirectly, to the root node.
  • lowerBound will be between 0 and 99, inclusive.
  • upperBound will be between 1 and 100, inclusive.
  • lowerBound will be strictly less than upperBound.
  • No event's likelihood will be within 1e-9 of lowerBound or upperBound.

Examples

  1. {"40","0 70 10"}

    30

    50

    Returns: { 0, 1 }

    This is the example from the problem statement. The probability of event 0 is 0.4, and the probability of event 1 is 0.34, both of which are within the specified range.

  2. {"20","2 50 50","0 50 50"}

    49

    51

    Returns: { 1, 2 }

    Both event 1 and event 2 have 50% probabilities of happening, regardless of what happens at their parents.

  3. {"10","0 99 41","1 40 3","2 91 43"}

    81

    88

    Returns: { }

    event | probability (rounded) ------+------------ 0 | 0.10 1 | 0.47 2 | 0.20 3 | 0.53

  4. {"81","0 54 56","0 15 26","1 93 63"}

    99

    100

    Returns: { }

  5. {"60","0 48 1","1 43 58"}

    48

    50

    Returns: { }

  6. {"25","0 79 99","1 12 96","2 85 67"}

    65

    98

    Returns: { 1, 3 }

  7. {"40","0 24 96","0 45 12","1 40 8","2 34 83"}

    78

    97

    Returns: { }

  8. {"79","0 64 52","1 70 87","0 38 99","1 24 8"}

    47

    81

    Returns: { 0, 1, 2, 3 }

  9. {"94","0 15 16","0 16 8","0 40 7"}

    6

    72

    Returns: { 1, 2, 3 }

  10. {"27","0 31 72"}

    13

    69

    Returns: { 0, 1 }

  11. {"56","0 14 59","0 93 95","2 43 35","2 52 54"}

    12

    79

    Returns: { 0, 1, 3, 4 }

  12. {"74","0 99 33"}

    55

    100

    Returns: { 0, 1 }

  13. {"98","0 27 45","1 87 65","0 50 89","2 20 98","2 54 15","5 88 60","1 33 19","0 36 27","2 39 32","7 1 33","2 55 55","0 64 72","6 78 44","7 16 33","3 90 99","12 31 54","8 21 14","16 48 53","2 56 29","5 44 40","5 59 84","10 37 48","21 65 12","16 86 37","4 86 6","20 27 39","26 90 86","21 79 85","13 37 26","29 83 35","18 44 59","6 5 4","16 79 25","29 86 18","15 60 35","32 63 15","33 22 92","29 46 77"}

    48

    82

    Returns: { 2, 3, 6, 11, 12, 13, 18, 19, 21, 23, 24, 28, 30, 31, 35, 37, 38 }

  14. {"45","0 22 7","1 83 32","1 7 67","2 91 43","1 11 31","0 76 9","6 7 94","2 17 37","5 5 49","2 3 98","10 70 13","10 15 4","6 22 50","5 29 72","9 34 77","6 16 63","10 31 48","9 86 87","0 19 43","3 53 47","16 42 1","3 40 67","1 70 18","8 37 7","5 95 93","21 91 65","2 36 78","20 4 83","22 47 21","7 62 84","23 99 68","8 55 33","19 38 54","0 75 60","5 80 45","31 31 75","1 33 78","23 98 87","8 55 14","38 35 55","33 78 68","41 21 97","13 81 93","18 53 41"}

    52

    61

    Returns: { 3, 7, 10, 14, 35 }

  15. {"27","0 5 3","0 6 13","1 82 32","0 62 24","1 78 69","1 55 47","2 23 5","0 73 45","2 89 87","3 30 55","0 48 61","1 84 44","8 9 2"}

    25

    46

    Returns: { 0, 3, 4, 12 }

  16. {"2","0 27 23","1 91 49","2 45 22","3 14 54","2 21 47","5 49 12","5 34 7","5 26 41","2 75 37","3 60 80","2 68 36","1 13 24","3 66 76","7 58 61","9 40 67","9 98 96","10 12 30","2 56 91","17 50 75","15 91 37","1 77 9","19 52 14","1 8 90","5 16 15","2 17 73","8 4 59","14 82 65","10 7 11","23 38 38","6 89 29","6 47 82","11 28 8"}

    37

    50

    Returns: { 4, 22, 25, 26, 29, 30 }

  17. {"9","0 43 11","0 66 91","2 83 14","0 71 97","1 41 24","2 42 46","3 69 27","6 65 2","8 29 77","3 37 96","1 5 6","7 70 9","3 51 84","8 96 24","13 81 13","12 91 63","8 22 53","2 68 63","9 72 42","7 34 97","3 65 22","19 70 87","6 78 45","21 19 35","0 2 99","24 75 8","21 13 59","14 3 66","13 37 88","8 32 89","9 79 71","22 17 13","17 24 95","10 83 12","29 66 27","15 69 44","2 4 64","20 47 96","24 23 21","33 1 15","32 41 1","23 94 98","14 77 52","39 41 53","30 47 48","45 47 63","24 94 40","20 13 74"}

    43

    59

    Returns: { 7, 10, 12, 14, 15, 17, 21, 29, 34, 35, 36, 44, 45, 46, 47 }

  18. {"41","0 53 19","1 88 43","2 44 75","0 75 57","4 66 57","3 48 62","3 29 12","2 98 77","7 15 96","9 22 73","0 96 30","5 11 62","12 58 73","3 55 12","10 7 82","5 2 66","5 11 42","2 46 89","14 19 27","1 50 44","16 34 98","21 9 21","11 46 91","21 79 51","16 98 32","18 99 46","16 74 95","16 37 33","14 21 33","15 44 3","20 1 1","8 45 7","25 86 72","11 82 10","30 47 49","28 65 12","25 5 35","8 57 51","28 19 37","8 80 28","34 72 84"}

    50

    57

    Returns: { 6, 34, 38 }

  19. {"7","0 64 62","0 55 3","1 49 69","1 9 46","3 79 69","1 72 74","0 42 42","2 91 96","2 87 72","9 86 62","0 64 89","6 17 1","7 13 80","11 7 38","5 14 69","1 79 82","1 82 37","4 77 46","0 83 90","2 52 70","18 72 19","19 78 57","15 46 62","14 64 98","20 90 65","4 89 28","19 72 43","5 73 47","27 63 46","3 43 87","18 80 93","30 37 7","0 9 41","7 49 67","28 24 23","19 71 25","28 33 60","27 2 39","13 66 17","1 46 45","38 75 32","16 55 22","6 75 10","37 99 76","4 71 30","33 76 76","40 71 39","42 94 42"}

    68

    87

    Returns: { 5, 6, 9, 10, 16, 20, 22, 25, 27, 31, 44, 46 }

  20. {"35","0 10 57","0 12 68","0 97 4","1 79 59","4 18 21","2 47 74","0 84 44","2 37 64","2 17 13","3 63 52","3 18 91","3 46 25","3 31 34","11 86 29","1 8 47","7 53 32","16 25 98","14 45 64","4 95 76","19 75 69","13 7 29"}

    33

    63

    Returns: { 0, 1, 2, 3, 6, 7, 8, 10, 16, 18 }

  21. {"24","0 40 91","1 22 43","1 11 14","1 81 54","1 69 76"}

    19

    71

    Returns: { 0, 2, 5 }

  22. {"62","0 40 26","0 60 88","2 94 60","0 33 12","4 65 71","2 47 52","2 73 61","6 30 87","6 43 68","4 33 22","8 78 75","4 25 65","5 79 14","7 38 42","11 68 67","11 2 98","10 47 87","14 76 88","6 41 33","5 6 86","10 26 64","18 63 94","9 58 97","7 37 12","14 99 23","3 2 79","24 73 91","7 62 55","8 98 47","28 54 30","6 43 33","14 54 99","16 75 11","19 4 75","10 78 38","1 9 62","6 65 56","32 83 76","22 16 91","34 70 34","28 72 22","41 38 5","23 79 92","13 22 72","30 98 90","32 15 20"}

    25

    72

    Returns: { 0, 1, 2, 4, 5, 6, 7, 8, 9, 12, 13, 14, 15, 19, 20, 21, 22, 24, 25, 28, 30, 31, 33, 34, 35, 36, 37, 39, 40, 41, 44 }

  23. {"56","0 5 11","0 87 16","1 6 20","3 91 60","0 70 6","5 56 64","2 92 64","2 98 21","0 15 24"}

    59

    72

    Returns: { 4, 6, 8 }

  24. {"51","0 70 76","1 76 53","0 92 57","1 31 2","4 56 16","1 90 68","2 27 19","6 69 24","6 63 46","5 72 51","9 72 88","8 53 23","9 59 30","7 88 12","1 48 78","4 42 69","12 13 12","3 7 71","4 98 70","1 88 16","18 62 24","15 78 5","21 20 61","22 63 83","1 36 7"}

    20

    53

    Returns: { 0, 4, 5, 7, 12, 13, 14, 18, 21, 22, 23, 25 }

  25. {"45","0 24 10","1 6 62","1 70 41","2 25 23","0 28 81","4 39 81","4 66 15","2 62 10","8 46 61","7 41 46","9 8 42","11 48 54","4 72 45","7 51 47","5 34 97","2 11 42","3 9 43","1 97 2","13 84 40","5 82 20","7 89 95","17 95 70","6 19 48","11 29 80","14 68 93","6 10 84","9 23 50","9 78 27","22 83 44","24 22 39","1 24 73","26 47 72","10 63 82","18 19 71","27 93 54"}

    62

    75

    Returns: { 6, 19, 24, 29, 31, 32, 33, 35 }

  26. {"86","0 34 20","1 74 47","2 95 29","1 13 74","4 80 91","0 60 52","3 35 60","1 6 60","5 27 34","8 90 39","4 92 17","4 56 85","6 75 53","8 34 57","1 12 43","13 7 78","11 86 23","4 4 90","6 15 83","19 74 59","11 22 77","7 4 33","18 56 23","11 42 18","16 45 80","25 93 65","16 87 93","25 56 43","26 36 70","22 22 89","1 6 43","5 90 30","3 62 1","29 85 19","20 3 19","8 71 41","28 79 92","25 91 74","10 56 49"}

    11

    93

    Returns: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 36, 37, 38, 39 }

  27. {"64","0 20 18","0 24 55","0 40 45","3 16 67","0 16 64","2 75 17","0 20 37","5 23 55","8 68 59","0 77 26","4 56 9","11 83 1"}

    10

    56

    Returns: { 1, 2, 3, 4, 5, 6, 7, 8, 11, 12 }

  28. {"89","0 86 89","0 38 13"}

    76

    91

    Returns: { 0, 1 }

  29. {"12","0 18 42","1 95 27","0 6 60","1 42 83","2 74 77","3 63 51","4 7 40","7 99 85","8 77 92","5 4 48","3 41 73","3 10 85","11 70 34","2 95 73","9 30 3","9 48 59","4 35 9","16 96 3","9 31 55","19 31 65","16 30 17","10 65 71","11 46 49","11 51 52","13 39 67","24 67 40","18 74 38","16 97 52","13 65 82","1 65 28","12 93 57","0 93 35","31 46 73","30 28 8","10 93 64","2 54 4","0 9 66","23 87 82","26 62 43","32 2 66","38 10 90","11 82 7","19 7 84","42 46 68"}

    28

    96

    Returns: { 1, 2, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 16, 18, 19, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 35, 36, 37, 38, 39, 40, 42, 43, 44 }

  30. {"54","0 33 98","0 12 56","1 28 73","3 26 24","2 86 74","3 72 21","0 70 47","4 66 60","8 38 2","2 19 95","9 30 42","1 3 67","6 48 69","5 3 81","12 93 67","0 7 16","14 27 31"}

    25

    70

    Returns: { 0, 1, 2, 3, 6, 7, 8, 11, 12, 13, 17 }

  31. {"37","0 61 49","0 61 33","1 56 67","1 68 21","1 50 49","0 94 80","5 37 84","1 36 74","6 15 17","1 10 51","0 95 50","7 37 76","1 84 41","1 94 93","8 1 67","8 21 27","4 58 99","13 30 22"}

    78

    98

    Returns: { 6, 14, 17 }

  32. {"41","0 42 7","0 3 11","2 50 47","0 96 67","2 12 40","0 36 62","5 60 59","5 66 25","2 64 96","3 51 56","0 16 98","4 94 29","3 97 12","0 37 24","0 65 98","4 88 97","0 37 26","0 91 61","2 62 13"}

    11

    32

    Returns: { 1, 14, 17, 19 }

  33. {"85","0 47 91","1 54 50","0 79 19","1 27 21","0 33 87","3 39 11","1 64 83","3 81 71","6 30 39","5 71 2","8 62 51","11 28 2","6 10 84","5 55 33","10 53 35","0 32 38","8 44 32","12 70 96","16 42 3","6 14 24","13 94 86","10 90 25","13 68 67","11 6 41","6 81 17","3 59 63","9 44 26","25 62 64","9 15 85","0 12 50","8 9 79","1 43 69","16 46 49","24 88 39","4 81 8","31 7 50","30 79 56","25 86 7","8 63 14","0 86 91","24 59 98","12 3 46","27 68 14","36 5 38","26 34 85","39 42 46","29 22 86","17 59 74","29 35 53"}

    58

    96

    Returns: { 0, 3, 7, 8, 11, 13, 18, 21, 23, 26, 28, 29, 37, 40, 41, 48 }

  34. {"14","0 97 36","1 94 35","0 34 36","3 57 72","3 50 63","4 99 88","3 61 3","1 85 75","7 89 25","6 48 12","8 76 46","6 66 69","12 82 23","6 93 97","1 26 86","12 84 3","2 2 2","12 46 97"}

    21

    78

    Returns: { 1, 2, 3, 4, 5, 7, 9, 10, 11, 12, 13, 15, 16, 18 }

  35. {"46","0 51 50","0 91 28","2 57 59","0 31 63","2 98 90","2 79 79","0 7 35","6 1 37","3 2 73","0 29 16","2 23 16","3 2 90","0 15 76","7 46 90","9 85 97","12 91 84","15 77 72","16 80 15","6 24 59","4 81 48","4 57 71","14 56 3","9 36 11","2 28 91","11 58 28","23 75 43","18 69 70","10 27 83","28 5 52","23 86 29","3 43 21","31 24 23","13 58 88","12 60 14","21 27 67","15 60 9","11 8 48","33 76 63","29 11 51","4 37 65","22 41 70","25 79 15"}

    87

    97

    Returns: { 5, 15 }

  36. {"55","0 99 32","0 3 14","0 10 13","0 19 2","4 70 51","4 79 88","0 46 11","1 73 63","1 71 49","7 36 20","3 32 21","4 34 60","8 86 59","1 59 33","8 85 50","10 82 32","11 65 41"}

    58

    97

    Returns: { 1, 6, 8, 9, 13, 15 }

  37. {"79","0 67 90","1 38 73","0 73 67","3 11 66","4 48 59","2 63 71","2 83 81","7 16 4","8 44 17","4 61 31","1 89 9","7 96 19","0 10 1","12 1 9","9 92 89","2 3 35","14 24 33","11 87 35","18 49 31","3 47 70","9 87 20","0 57 29","9 86 99","10 43 42","9 72 55"}

    11

    84

    Returns: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 16, 17, 18, 19, 20, 21, 22, 24, 25 }

  38. {"30","0 50 3","0 75 45","2 79 98","2 38 26","3 28 21","1 98 78","4 55 67","1 21 98","0 34 53","9 39 87","3 91 89","11 80 42","4 25 94","8 81 79"}

    37

    88

    Returns: { 2, 3, 6, 7, 8, 9, 10, 12, 13, 14 }

  39. {"78","0 65 9","0 94 84","1 45 11","0 77 31","1 34 18","0 65 68","3 83 67","5 63 53","8 57 3","2 97 74","7 97 47","5 72 39","5 54 48","8 69 59","1 20 21","1 10 61","8 8 28","2 32 87","0 43 20"}

    38

    70

    Returns: { 1, 4, 6, 8, 12, 13, 14 }

  40. {"33","0 56 39","0 51 36","2 60 74","1 95 64","4 80 10","5 15 24","1 1 13","0 22 96","1 95 44","5 98 22","8 58 62","7 94 38","11 87 68","10 81 83","3 63 49","14 63 72","14 70 81","14 95 19","12 29 51","19 97 40","8 38 23","14 73 27","14 83 31","12 23 53","16 25 41","0 9 95","18 96 33","10 89 67","3 88 78","19 45 17","22 10 48","16 34 68","29 45 78","3 13 65","34 6 31"}

    66

    92

    Returns: { 3, 4, 8, 9, 10, 13, 14, 17, 18, 23, 26, 27, 28, 29 }

  41. {"47","0 68 58","1 42 81","2 9 57","0 51 55","0 71 80","4 79 42","1 86 53","1 31 41","8 71 80","5 65 53","3 56 64","6 88 7","6 6 46","13 36 85","10 44 40","11 44 93","10 95 3","15 18 67","4 6 57","9 4 65","0 86 68"}

    66

    95

    Returns: { 5, 7, 9, 14, 21 }

  42. {"49","0 35 98","1 80 2","0 95 83","3 90 75","3 59 79","0 12 12","5 14 40","3 94 18","5 76 6","7 15 32","4 12 8","3 58 28","11 41 62","7 39 11","9 87 45","0 81 99","8 9 80","15 11 18","6 38 34"}

    33

    80

    Returns: { 0, 1, 2, 5, 9, 12, 13, 15, 19 }

  43. {"51","0 80 21","1 80 86","0 51 77","1 7 85","3 69 10","1 70 28"}

    16

    92

    Returns: { 0, 1, 2, 3, 4, 5, 6 }

  44. {"8","0 22 27","1 11 86","0 47 8","1 86 31","1 24 87","3 81 47","4 19 74","5 47 2","1 79 27","5 77 26","1 23 69","5 4 22","1 80 37","11 82 55","4 70 36","5 7 53","5 77 79","7 11 77","17 51 43","5 56 45","5 54 55","16 29 75","11 99 50","8 21 48","2 52 17"}

    56

    96

    Returns: { 2, 5, 10, 11, 14, 17, 22, 23 }

  45. {"38","0 2 16","1 50 27","2 89 9","3 68 84","0 45 36","0 71 12","0 39 69","5 90 33","8 12 70","6 84 18","3 60 35","0 26 2","2 88 59","11 9 69","10 61 68","13 11 74"}

    4

    42

    Returns: { 0, 1, 2, 3, 5, 6, 9, 10, 12, 16 }

  46. {"82","0 1 55","1 42 77","1 51 46","1 72 76","3 17 74","4 82 27","5 17 53","0 62 91","2 5 95","5 23 88","7 59 51","7 6 10","10 61 54","10 59 55","9 91 6","9 47 50","12 2 86","12 8 15","18 43 33","16 37 71","19 47 51","18 19 43","20 74 81","21 12 64","5 94 57","16 30 29","4 98 63","23 17 59","3 33 82","4 57 50","21 48 86","26 8 8","14 89 58","24 67 6","11 57 67","24 14 41","20 55 25","33 65 14","36 95 21","10 9 53","16 50 72","31 22 39","21 36 48","33 26 12","16 37 82","6 11 33","28 71 49","39 46 84"}

    30

    93

    Returns: { 0, 2, 3, 4, 5, 6, 7, 8, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 23, 24, 25, 27, 29, 30, 31, 33, 35, 36, 37, 38, 39, 41, 43, 45, 47, 48 }

  47. {"28","0 86 71","0 16 24","2 82 68","1 22 54","2 93 80","1 89 52","1 15 55","4 73 54","8 9 42","6 97 61","3 4 62","0 90 82","10 60 65","6 75 55","2 10 72","12 30 73","16 91 45","17 42 78","2 68 74","13 80 26","17 2 4","4 47 95","11 24 75","10 52 43","22 76 47","20 28 32","11 67 49","4 19 55","22 25 12","20 44 59","29 68 16","5 59 71","28 73 1","10 57 6","2 58 68","17 76 1","17 38 80","3 65 19","5 76 48","36 7 77","15 84 28","32 66 68","26 33 37","20 54 50","2 19 60","25 18 5","32 19 61","35 94 74","15 21 34"}

    20

    79

    Returns: { 0, 1, 2, 3, 4, 7, 8, 9, 11, 13, 14, 15, 16, 17, 18, 19, 20, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 47, 49 }

  48. {"22","0 34 47","0 20 85","2 36 5","2 21 67","4 99 30","5 37 54","1 13 50","0 13 92"}

    58

    82

    Returns: { 2, 8 }

  49. {"10","0 76 23","0 52 64","0 79 47","0 59 59","4 57 30","1 71 13","0 70 54","6 98 65","6 19 92","7 81 8","0 12 88","5 56 88","12 22 43","3 21 35","14 15 40","8 70 6","6 71 71","8 19 92","12 16 13","1 30 87","1 72 46","18 69 61","21 53 40","9 73 48","11 88 29","2 6 81","21 84 45","0 96 84","17 45 81","25 44 47","28 31 4","5 84 23","4 16 29","9 80 20","3 15 10","31 57 84","6 16 37","20 63 99","0 91 34","20 74 74","16 15 3"}

    69

    82

    Returns: { 8, 9, 11, 12, 17, 20, 25, 36, 38, 40 }

  50. {"41","0 31 30","1 26 55","1 52 7","2 74 83","0 43 93","0 71 29","3 33 91","7 74 63","6 27 43","2 57 11","6 90 74","11 49 84","0 1 46","1 46 67","2 14 47","1 98 66","15 76 38","6 24 65","14 14 29","13 29 41","3 40 81","3 93 30","22 39 63","3 84 99","2 9 37","18 21 10"}

    12

    77

    Returns: { 0, 1, 2, 3, 5, 6, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 26 }

  51. {"38","0 32 5","0 73 87","1 57 10","2 4 28","3 89 23","1 14 73","4 58 78","4 24 27","4 34 13","8 77 75","1 97 30","1 82 68","2 55 55","2 15 98","5 4 14","12 35 13","14 91 69","5 56 80","9 35 43","11 65 13","0 70 62","16 65 63","17 1 22","21 12 53","4 36 4","3 4 95","10 93 67","10 75 59","28 59 29","13 16 72","6 95 90","27 91 32","29 42 76","2 44 34","19 81 52"}

    56

    80

    Returns: { 6, 7, 10, 12, 17, 18, 21, 22, 26, 28, 33, 35 }

  52. {"57","0 76 85","1 50 12","0 67 85","2 8 98","1 58 32","5 8 20","2 68 98","6 78 98","8 92 79","0 97 20","7 46 25","6 68 42","4 71 9","4 39 25","11 7 57","12 18 2"}

    25

    95

    Returns: { 0, 1, 2, 3, 4, 5, 7, 9, 10, 11, 12, 13, 14, 15 }

  53. {"90","0 6 78","0 1 12","0 26 57","3 84 64","1 74 4","4 40 6","4 62 50","7 2 86","3 14 93","6 73 73","9 88 5","3 93 28","9 18 87","13 62 42","2 52 44","2 9 2","15 27 21","5 60 24","5 28 41","16 15 63","2 58 88","20 21 69","17 75 60","8 59 90","10 55 63","24 51 84","1 80 32","1 28 63","2 34 94","2 21 63","20 51 57","24 42 28","28 2 54","17 77 5","26 36 86","25 96 12","29 68 70","19 14 47"}

    5

    43

    Returns: { 1, 3, 5, 6, 8, 13, 17, 18, 19, 22, 27, 32, 33, 34, 38 }

  54. {"83","0 39 11","0 19 4","0 51 42","2 55 11","3 41 4","5 94 60"}

    20

    61

    Returns: { 1, 3, 5 }

  55. {"34","0 93 29","0 69 15","2 28 1","3 86 51","4 92 67","1 77 77","0 33 9","5 86 90","4 84 6","3 59 89","7 54 19","3 86 54","10 81 81","9 61 38","9 80 23","7 87 4","5 52 14","17 86 1","9 80 34","6 60 55","9 62 6","9 3 3","4 70 95","17 78 4","4 39 32","18 38 62","21 95 19","1 25 33","17 94 86","17 38 10","0 68 65","15 76 97"}

    43

    97

    Returns: { 1, 4, 5, 6, 8, 9, 10, 12, 13, 14, 15, 17, 19, 20, 23, 26, 27, 29, 31, 32 }

  56. {"93","0 84 42","1 81 86","2 89 74","2 20 23","3 96 45","5 81 59","1 81 24","2 16 2","0 4 45","3 44 37","0 52 71","8 22 48","9 88 34","1 34 91","8 17 13","2 99 30","4 32 5","3 51 38","14 87 11","2 52 76","13 63 37","1 30 41","17 25 84","0 59 5","17 98 24","7 20 50","10 98 46","10 51 69","23 88 23","14 69 50","25 75 2","4 41 55","24 87 33","6 94 18","30 12 58"}

    61

    69

    Returns: { 27, 28, 33 }

  57. {"35","0 12 91","1 82 22","1 96 27","2 15 83","4 58 39","0 26 73","6 11 84","6 16 47","6 93 22","8 61 51","3 75 93","10 33 96","6 74 27","7 5 99","11 58 11","4 62 19","11 7 81","5 72 97","5 58 49","0 90 44","19 93 59","9 8 77","21 29 91","15 34 48","7 88 87","20 6 89"}

    31

    57

    Returns: { 0, 4, 5, 6, 7, 10, 13, 15, 16, 19, 22, 23, 24, 26 }

  58. {"93","0 99 24","0 17 5","1 14 40","2 16 96","0 70 38","0 29 51","2 64 78","2 83 82","6 55 73","1 81 86","1 62 71","2 60 10","5 10 38","13 64 80","5 98 67","7 56 12","7 85 86","3 16 50","13 62 72","3 9 58","5 24 55","13 14 70","6 41 36","4 42 87","17 99 32","2 50 89","10 37 45","24 55 58","4 77 49","24 62 39","1 16 25","23 36 81","19 31 78","7 51 27","9 13 89","30 89 12","27 63 91","36 95 70","7 37 6","8 16 85","32 32 45","13 46 7"}

    69

    89

    Returns: { 4, 7, 8, 10, 14, 15, 17, 19, 26, 29, 37, 38 }

  59. {"80","0 63 85","0 44 4","1 15 48","3 29 15","1 75 61","4 31 54","6 71 18","3 90 4","8 78 77","7 75 70","3 37 11","7 3 66","11 23 50","4 5 27","0 15 11","1 43 24","2 48 74","4 66 48","10 63 69","16 80 9","0 12 78","2 67 15","7 39 65","6 48 54","0 73 63","3 90 22","12 49 49","11 9 52","27 4 99","7 51 8","19 56 93","18 36 62","26 48 36","20 66 35","26 18 61","0 4 5","13 46 12"}

    21

    77

    Returns: { 1, 2, 3, 5, 6, 7, 8, 10, 12, 13, 14, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 37 }

  60. {"14","0 61 78","0 52 80","2 16 3","0 79 93","2 94 34","3 31 65","0 13 11","5 66 97","8 28 85"}

    19

    64

    Returns: { 6, 9 }

  61. {"44","0 90 34","0 61 67","1 40 22","3 58 70","4 55 44","1 13 84","2 96 61","7 10 59","8 7 31","6 46 9","5 99 58","11 7 80","12 59 94","3 26 80","13 1 53","8 61 13","9 21 69","14 68 81","2 90 15","12 35 69","2 27 40","8 41 63","10 1 99","2 51 29","0 27 95","9 65 36","11 30 32","2 86 54","18 61 96","17 7 32","14 19 67","5 9 90","16 15 28","1 70 89","2 37 41","15 71 61","14 49 2","11 57 96","18 47 92","27 9 97","12 42 16","6 43 68"}

    41

    51

    Returns: { 0, 6, 24, 26, 32 }

  62. {"33","0 94 5","1 2 48","2 37 56","2 29 38","3 30 50","5 38 1","3 85 46","3 97 19","4 95 80","5 97 77","1 22 43","0 9 30","7 92 52","7 44 65","6 12 46","4 44 72","4 17 40","16 51 57","10 52 76","6 53 13","3 99 56","1 96 54","13 70 32","9 85 75","6 14 91","10 17 40","0 7 10","6 47 79","15 10 72","5 76 30","24 36 25","28 6 40","9 81 34","15 11 62","5 31 1","17 92 76","20 49 52","24 93 16","33 71 46","14 64 45","25 54 66","7 28 2","5 15 21","36 59 36","44 51 41","37 45 43","29 45 88"}

    5

    99

    Returns: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47 }

  63. {"90", "8 11 19", "0 58 54", "8 18 9", "0 96 35", "1 70 22", "0 40 1", "6 78 2", "2 74 29"}

    7

    42

    Returns: { 1, 3, 5, 6, 7 }

  64. {"70", "5 12 19", "9 45 37", "10 83 33", "3 59 58", "0 75 44", "10 25 24", "6 64 47", "13 34 79", "5 13 32", "0 9 34", "10 37 4", "1 54 80", "12 62 39", "9 67 49", "3 6 58"}

    30

    61

    Returns: { 2, 3, 4, 7, 8, 13, 14, 15 }

  65. {"51", "29 58 3", "6 56 86", "18 97 1", "44 99 25", "33 69 90", "27 67 49", "32 15 19", "33 1 21", "45 12 33", "29 24 40", "45 86 74", "40 30 65", "0 18 27", "1 90 65", "0 47 62", "40 81 72", "42 25 56", "45 16 81", "8 94 92", "29 41 92", "24 4 29", "32 56 91", "20 16 77", "1 35 79", "45 77 61", "6 50 19", "20 69 43", "4 6 16", "15 55 26", "42 73 90", "40 8 49", "33 16 33", "15 95 47", "9 66 40", "25 80 39", "35 72 70", "27 10 36", "40 36 10", "32 2 48", "33 44 23", "22 51 45", "25 8 43", "18 32 96", "45 41 74", "0 51 6", "18 48 15"}

    8

    82

    Returns: { 0, 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 23, 24, 25, 26, 27, 28, 29, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 }

  66. {"74", "13 21 67", "0 96 8", "7 96 2", "14 46 41", "21 88 59", "0 32 99", "2 98 26", "7 95 29", "21 67 53", "11 30 8", "0 17 70", "9 10 2", "9 29 36", "7 98 44", "11 73 52", "9 55 29", "11 79 56", "9 15 92", "0 78 82", "0 27 69", "0 14 75"}

    24

    99

    Returns: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 14, 15, 16, 17, 18, 19, 20, 21 }

  67. {"66", "2 6 34", "9 87 24", "9 33 55", "9 78 25", "16 70 73", "8 37 29", "34 9 50", "7 6 86", "8 32 28", "15 14 93", "7 16 24", "22 71 91", "11 43 36", "16 57 15", "9 95 93", "0 91 67", "22 68 41", "29 54 62", "14 44 16", "33 29 89", "11 6 5", "16 35 21", "10 80 42", "7 92 66", "6 69 48", "27 50 23", "33 56 21", "16 35 39", "7 85 71", "6 62 93", "11 67 68", "4 42 84", "15 53 49", "0 32 2", "7 77 50", "16 84 67", "34 65 76", "6 1 68", "12 54 33"}

    0

    70

    Returns: { 0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 13, 14, 17, 18, 19, 20, 21, 22, 23, 25, 26, 27, 28, 31, 32, 33, 34, 35, 38, 39 }

  68. { "51", "29 58 3", "6 56 86", "18 97 1", "44 99 25", "33 69 90", "27 67 49", "32 15 19", "33 1 21", "45 12 33", "29 24 40", "45 86 74", "40 30 65", "0 18 27", "1 90 65", "0 47 62", "40 81 72", "42 25 56", "45 16 81", "8 94 92", "29 41 92", "24 4 29", "32 56 91", "20 16 77", "1 35 79", "45 77 61", "6 50 19", "20 69 43", "4 6 16", "15 55 26", "42 73 90", "40 8 49", "33 16 33", "15 95 47", "9 66 40", "25 80 39", "35 72 70", "27 10 36", "40 36 10", "32 2 48", "33 44 23", "22 51 45", "25 8 43", "18 32 96", "45 41 74", "0 51 6", "18 48 15" }

    8

    82

    Returns: { 0, 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 23, 24, 25, 26, 27, 28, 29, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 }

  69. { "51", "29 58 3", "6 56 86", "18 97 1", "44 99 25", "33 69 90", "27 67 49", "32 15 19", "33 1 21", "45 12 33", "29 24 40", "45 86 74", "40 30 65", "0 18 27", "1 90 65", "0 47 62", "40 81 72", "42 25 56", "45 16 81", "8 94 92", "29 41 92", "24 4 29", "32 56 91", "20 16 77", "1 35 79", "45 77 61", "6 50 19", "20 69 43", "4 6 16", "15 55 26", "42 73 90", "40 8 49", "33 16 33", "15 95 47", "9 66 40", "25 80 39", "35 72 70", "27 10 36", "40 36 10", "32 2 48", "33 44 23", "22 51 45", "25 8 43", "18 32 96", "45 41 74", "0 51 6", "18 48 15" }

    33

    89

    Returns: { 0, 2, 3, 4, 5, 6, 10, 11, 12, 14, 15, 16, 17, 18, 20, 22, 23, 24, 25, 26, 27, 29, 30, 31, 33, 34, 35, 36, 39, 40, 41, 43, 44, 46 }

  70. { "40", "0 70 10" }

    30

    50

    Returns: { 0, 1 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: