Statistics

[Note to plug-in users: This problem statement contains images and superscripts. If you do not see the images, or if 2^k is displayed the same as 2k, then please view the problem in the applet.]

A Hilbert curve is a path that traces through all the points in a two-dimensional square grid in such a way that each step in the path moves between neighbors in the grid. Hilbert curves are sometimes used in image processing because they exhibit greater locality than other common methods of linearizing a two-dimensional image, such as row-by-row (even than the boustrophedonic variations of row-by-row that alternate between left-to-right and right-to-left).

A rank-k Hilbert curve is a path through a 2^k-by-2^k grid. A rank-1 Hilbert curve is a simple U-shape through a 2-by-2 grid, as shown below.



The blue point indicates the first point in the path and the red point indicates the last point in the path. For k > 1, a rank-k Hilbert curve is composed of four rank-(k-1) Hilbert curves, shown below as dotted lines.



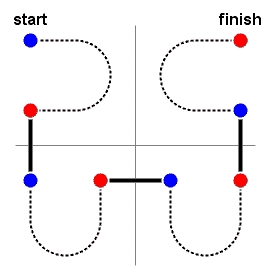
Notice how the curve is organized in quadrants, first the upper left, then the lower left, then the lower right, and finally the upper right. (The cross in the background is not part of the curve; it merely highlights the quadrants.) Notice also how some of the rank-(k-1) curves are flipped and rotated compared to the orientation of the rank-k curve. The blue and red points indicate where each rank-(k-1) curve begins and ends, respectively. The overall rank-k curve begins at the first point of the upper left rank-(k-1) curve and ends at the last point of the upper right rank-(k-1) curve. 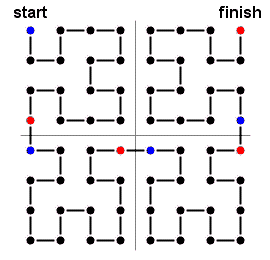Here is a complete picture of a rank-3 Hilbert curve.

You will be given a value k and coordinates x and y in a 2^k-by-2^k grid. Coordinates range from 1 to 2^k inclusive, with the upper left corner at coordinates (1,1). Assuming the points are traversed in the order specified by a rank-k Hilbert curve, determine how many steps it takes to reach the point at coordinates (x,y). For example, it takes 0 steps to reach the upper left corner at coordinates (1,1) and 4^k-1 steps to reach the upper right corner at coordinates (2^k,1).