Problem Statement
Plugin users: There is a picture in the problem statement.
Given a circular sequence of integers, calculate the maximum sum of a (contiguous) sequence of these numbers. You should also calculate how many different sequences yield this maximum sum. Two sequences are different if they don't contain the same elements from the original sequence (see example 1). At least one integer in the circular sequence will be positive (greater than zero).
For instance, consider the circular sequence in the picture below.
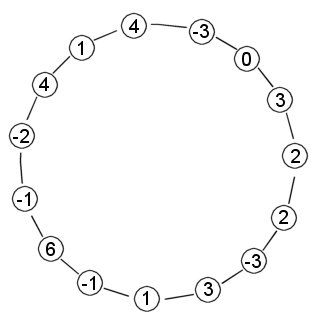
There are four different ways to select a sequence of integers so the sum becomes 19 (which is the maximum sum):
0 3 2 2 -3 3 1 -1 6 -1 -2 4 1 4 3 2 2 -3 3 1 -1 6 -1 -2 4 1 4 3 1 -1 6 -1 -2 4 1 4 -3 0 3 2 2 4 1 4 -3 0 3 2 2 -3 3 1 -1 6
The circular sequence will be generated by the following formula: (a, b, c, d and n are parameters)
int seed = 0;
for(int i = 0; i < n; i++)
{
seed = (seed * a + b) % 32768;
int val =(seed * c) / 32768 - d;
// val is the i'th value in the circular sequence
}
Create a class CircularSequence containing the method maxSequence which takes
Definition
- Class:
- CircularSequence
- Method:
- maxSequence
- Parameters:
- int, int, int, int, int
- Returns:
- int[]
- Method signature:
- int[] maxSequence(int a, int b, int c, int d, int n)
- (be sure your method is public)
Notes
- The parameter c determines the span of the integers while d determines the lower bound. The range of the integers will thus be between -d and -d+c-1, inclusive.
Constraints
- a and b will be between 0 and 32767, inclusive.
- c will be between 2 and 1000, inclusive.
- d will be between 0 and c-2, inclusive.
- n will be between 1 and 1,000,000, inclusive.
- At least one integer in the circular sequence will be greater than zero.
- There will be at most 2,000,000,000 different contiguous sequences yielding the maximum sum.
Examples
8087
1869
10
3
15
Returns: { 19, 4 }
This is the example above.
1234
46
2
0
5
Returns: { 1, 11 }
The generated sequence is {0, 1, 0, 0, 0}. The maximum sum is obviously 1. There are 11 ways to get this sum: 1 way to select a single element: {1} 2 ways to select two elements: {0, 1} and {1, 0} 3 ways to select three elements: {0, 0, 1}, {0, 1, 0} and {1, 0, 0} 4 ways to select four elements: {0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0} and {1, 0, 0, 0} 1 way to select all five elements: {0, 0, 0, 0, 1} (or any rotation of this)
4810
8393
20
10
18
Returns: { 45, 1 }
These parameters yield the circular sequence {-5, -5, 7, 5, 0, 8, 1, 0, 6, 0, 1, 7, -10, -5, 5, 5, 5, 5}. The maximum value is achieved by taking all elements except -10 and -5 at the near end.
1943
3184
9
5
100000
Returns: { 14, 195 }
30001
15000
3
1
1000000
Returns: { 37, 8 }
1
10922
3
1
16383
Returns: { 1, 59645042 }
The generated sequence looks like this: {-1, 0, 1, -1, 0, 1, -1, 0, 1, ... }, i.e. the sequence {-1, 0, 1} is repeated 5461 times. The maximum sum is obviously 1. There are 2 essentially different ways to get this sum: Start at a 0, end at a 1. There are 5461 0's to start at, and 5461 1's to end at, i.e. 54612 ways. Start at a 1, end at a 1. Again there are 54612 such ways. There are thus 2 * 54612 = 59645042 ways to get the sum 1.
1
23482
3
1
438294
Returns: { 7, 1016928 }
1
23482
21
10
2999
Returns: { 65, 24 }
1
16384
4
1
89442
Returns: { 1, 1999967841 }
12767
32567
1000
500
100000
Returns: { 10021, 49 }
16327
6960
639
413
613876
Returns: { 1023, 1199 }
31805
19163
6
0
86064
Returns: { 215164, 17264 }
14591
15242
507
341
865208
Returns: { 290, 33797 }
18787
18405
35
0
56236
Returns: { 956479, 1667 }
2495
10124
850
730
613598
Returns: { 216, 2397 }
9311
23200
970
793
236716
Returns: { 629, 3699 }
9177
3520
616
286
958875
Returns: { 20048951, 1872 }
25449
28447
2
0
39162
Returns: { 19569, 39065 }
11599
9728
791
96
49815
Returns: { 10897501, 6226 }
32495
24592
284
199
479212
Returns: { 189, 1872 }
32292
4638
3
1
31930
Returns: { 3, 31925 }
25015
6254
5
2
71532
Returns: { 197, 612 }
7568
2996
5
2
6764
Returns: { 2, 6762 }
14632
30776
3
1
15980
Returns: { 1, 31956 }
20019
19527
5
2
417551
Returns: { 257, 150 }
9887
3185
5
2
967944
Returns: { 52, 2838 }
13631
25451
3
1
43550
Returns: { 22, 10500 }
32757
18954
3
1
778198
Returns: { 168, 3008 }
27691
31395
5
2
969664
Returns: { 331, 116 }
315
26380
3
1
21806
Returns: { 61, 150 }
20591
27968
9
4
10303
Returns: { 15, 812 }
29935
27635
3
1
923282
Returns: { 52, 6075 }
30683
29182
9
4
619100
Returns: { 277, 225 }
22823
17854
7
3
932253
Returns: { 129, 77634 }
29264
15595
953
297
2
Returns: { 665, 1 }
17225
10260
224
130
6
Returns: { 144, 1 }
26284
32176
975
93
9
Returns: { 3787, 1 }
11504
31371
31
21
3
Returns: { 13, 1 }
18477
11169
687
410
5
Returns: { 272, 1 }
23461
10719
115
10
18
Returns: { 820, 1 }
28781
30220
53
25
5444
Returns: { 5835, 1 }
23664
2895
886
653
3
Returns: { 24, 1 }
10890
25082
887
155
4
Returns: { 1402, 1 }
32621
7998
649
316
12544
Returns: { 93360, 1 }
3371
25109
940
665
9
Returns: { 555, 1 }
18721
21360
497
120
3
Returns: { 410, 1 }
7096
15548
9
4
6
Returns: { 2, 1 }
16215
13621
574
391
107
Returns: { 615, 1 }
13799
29062
27
7
6
Returns: { 50, 1 }
25085
18103
232
113
73
Returns: { 1256, 1 }
6319
3654
790
185
647
Returns: { 133015, 1 }
24825
32119
223
177
38
Returns: { 75, 1 }
8141
18378
435
308
8368
Returns: { 480, 1 }
22707
28792
910
171
104
Returns: { 33613, 1 }
20000
20000
456
0
1
Returns: { 278, 1 }
10000
10000
100
0
2
Returns: { 36, 1 }
17719
31254
319
303
870
Returns: { 15, 2 }
31955
21525
347
202
46242
Returns: { 1459, 3 }
29533
18637
190
48
88944
Returns: { 4135954, 3 }
12895
10651
517
446
431
Returns: { 131, 2 }
2937
380
204
8
12754
Returns: { 1192733, 3 }
32673
16857
818
578
96212
Returns: { 1347, 3 }
11473
32764
544
350
36290
Returns: { 1059, 4 }
25557
29403
951
179
78145
Returns: { 23150373, 3 }
32395
31513
460
328
39950
Returns: { 541, 3 }
20803
10817
412
83
65419
Returns: { 8012890, 4 }