Problem Statement
A hexagonal grid is a tiling of the plane consisting solely of regular hexagons. You will be given two pairs of coordinates, identifying two hexagons in the grid. Consider a line segment connecting the centers of these two hexagons, and return the number of hexagons that this line segment intersects.
Only count hexagons if the line passes through their interior. Do not count a hexagon if the line only intersects one of its corners or is coincident with one of its edges.
Hexagons will be identified by a pair of coordinates, as shown in the following diagram. The first coordinate is proportional to the horizontal distance from the vertical axis. The second coordinate is proportional to the vertical distance from the diagonal axis.
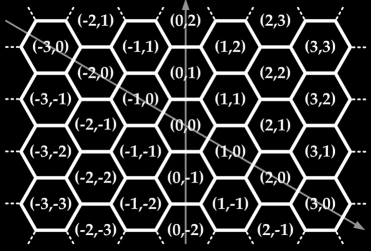
Definition
- Class:
- HexagonIntersections
- Method:
- count
- Parameters:
- int, int, int, int
- Returns:
- int
- Method signature:
- int count(int x0, int y0, int x1, int y1)
- (be sure your method is public)
Constraints
- x0, y0, x1, and y1 will be between -10000 and 10000, inclusive.
- (x0,y0) and (x1,y1) will not be the same point.
Examples
1
-2
3
1
Returns: 4
A line between the centers of hexagons (1,-2) and (3,1) intersects 4 hexagons:
0
0
1
0
Returns: 2
0
0
1
1
Returns: 2
0
0
0
1
Returns: 2
0
0
-1
0
Returns: 2
0
0
-1
-1
Returns: 2
0
0
0
-1
Returns: 2
11
10
10
10
Returns: 2
11
11
10
10
Returns: 2
10
11
10
10
Returns: 2
9
10
10
10
Returns: 2
9
9
10
10
Returns: 2
10
9
10
10
Returns: 2
4
2
0
0
Returns: 3
2
4
0
0
Returns: 3
-2
2
0
0
Returns: 3
-4
-2
0
0
Returns: 3
-2
-4
0
0
Returns: 3
2
-2
0
0
Returns: 3
0
0
4
-1
Returns: 6
0
0
10
2
Returns: 11
500
500
505
504
Returns: 6
3000
-2000
3012
-1985
Returns: 16
0
0
1
5
Returns: 6
0
0
-4
16
Returns: 21
4
5
-1
1
Returns: 6
20
0
0
-25
Returns: 26
-10000
-10000
10000
10000
Returns: 20001
-10000
-10000
10000
9999
Returns: 26666
-10000
-10000
9999
9998
Returns: 26666
-10000
10000
10000
-10000
Returns: 20001
-9999
10000
10000
-10000
Returns: 40000
-9999
9998
10000
-10000
Returns: 39998
9284
3473
2374
8372
Returns: 12480
-2375
9374
283
5478
Returns: 6967
-10000
51
10000
51
Returns: 20001
-10000
-51
10000
-52
Returns: 26668
-2004
-1002
-2000
-1000
Returns: 3
This line is coincident with the edges of several hexagons, but it only intersects the interior of three:
54
93
64
95
Returns: 11
0
0
19
20
Returns: 26
0
0
19
-20
Returns: 40
9999
3456
-9999
-9999
Returns: 22294
0
0
1
10000
Returns: 13334