Statistics

Note to plugin users: this problem contains images which may not display properly with some plugins

Figurate numbers are numbers which form a scalable pattern of nested geometric figures. The hexagonal numbers (1,6,15,28,45,66,91,120,153...) form the following figures with points arranged in a plane as nested hexagons.

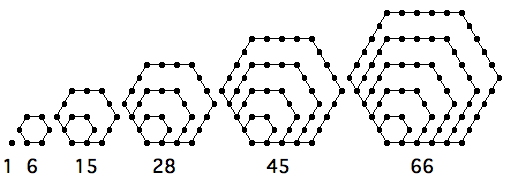
In the year 1830, the great mathematician, Legendre, proved that every integer larger than 1719 can be formed as the sum of exactly four hexagonal numbers (although many larger integers can also be formed as the sum of fewer than four hexagonal numbers). This was pretty much the last word on the subject until much later, in the year 1990, when this result was improved to three hexagonal numbers for all "sufficiently large" integers.

In this problem we ask the slightly different question: "what is the minimum number of hexagonal numbers that is required to form a particular sum?" Let's call this MLHS(n), for Minimum Length Hexagonal number Sum totaling to n. Here are the first few terms of MLHS(n):

n  MLHS(n)  a minimum length sum
1    1      1
2    2      1+1
3    3      1+1+1
4    4      1+1+1+1
5    5      1+1+1+1+1
6    1      6
7    2      1+6
8    3      1+1+6
9    4      1+1+1+6
10   5      1+1+1+1+6
11   6      1+1+1+1+1+6
12   2      6+6

For n greater than 1719, we know MLHS(n) <= 4 due to Legendre's result. But since our problem is different we can actually establish much tigher bounds. Six is the highest possible answer which only occurs for MLHS(11) and MLHS(26).
The largest n that has MLHS(n) = 6 is 26,
The largest n that has MLHS(n) = 5 is 130,
The largest n that has MLHS(n) = 4 is 146858.

Given a number, N, return MLHS(n), the minimum number of terms required to form a sum of N, when each term is a hexagonal number.