Statistics

Problem Statement for "DFAReversal"

Problem Statement

A Deterministic Finite Automata (DFA) is a finite state machine with some number of states which we will call states 0 through N-1. For the purposes of this problem, state 0 is the start state. The DFA is then given a sequence of symbols from a finite alphabet (an alphabet might contain only '0' and '1', for example, or might be only lowercase letters). For each state, there is a transition for each symbol in the alphabet to some state (possibly the same state). Finally, some set of states are denoted as accept states. If the DFA is in one of the accept states after a sequence of symbols has been given to it, then it accepts that sequence of symbols, otherwise it rejects the sequence.

For example, consider the simple DFA illustrated below:

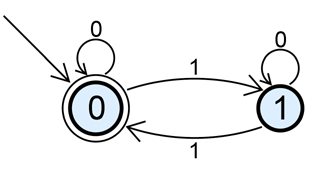
The DFA starts in state 0, and a '1' causes it to switch from state 0 to state 1 and vice versa, while a '0' causes it to remain in the same state. Since state 0 is the only accept state, a sequence is accepted if, and only if, there are an even number of '1's.

You will be given a DFA as a String[], dfa. Element i of dfa will represent state i, and be formatted as a list of K integers separated by single spaces, where K is the number of symbols in the alphabet. Integer j of element i of dfa indicates the state that the DFA will end up in if it is currently in state i, and is given symbol j. A int[], accept, indicates which states are accept states. Your task is, given the DFA specified by the input, return the minimum number of states required to build a new DFA that accepts the reverse of every sequence accepted by the input DFA. That is, the new DFA should accept a sequence s if, and only if, the input DFA accepts reverse(s).

Definition

Class:
DFAReversal
Method:
reverse
Parameters:
String[], int[]
Returns:
int
Method signature:
int reverse(String[] dfa, int[] accept)
(be sure your method is public)

Constraints

  • Each state in dfa will be reachable from the start state, state 0.
  • dfa will contain between 1 and 10 elements, inclusive.
  • Each element of dfa will contain between 1 and 10 integers separated by single spaces, with no extra leading zeros, inclusive.
  • Each element of dfa will contain the same number of integers.
  • Each integer in dfa will be between 0 and the number of elements in dfa-1, inclusive.
  • accept will contain between 0 and 10 elements, inclusive.
  • Each element of accept will be between 0 and the number of elements in dfa-1, inclusive.
  • No number will occur more than once in accept.

Examples

  1. {"0 1","1 0"}

    {0}

    Returns: 2

    In this DFA, we switch states whenever we see the second symbol. Since we start in state 0, and it is our accept state, this DFA accepts all strings with an even number of occurrences of the second symbol. Therefore, if s is accepted by this DFA, reverse(s) is also.

  2. {"0 1", "0 0"}

    {0,1}

    Returns: 1

    Everything is accepted, so we really only need one state.

  3. {"0 1", "0 2", "0 2"}

    {2}

    Returns: 4

    This DFA accepts any sequence that ends with two occurrences of the second symbol.

  4. {"1 1", "2 2", "3 3", "4 4", "5 5", "6 6", "7 7", "9 8", "8 8", "9 9"}

    {8}

    Returns: 256

  5. {"9 9", "1 1", "2 2", "1 2", "3 3", "4 4", "5 5", "6 6", "7 7", "8 8"}

    {2}

    Returns: 256

  6. {"1 1", "2 2", "3 3", "4 4", "5 5", "6 6", "7 7", "8 8", "0 9", "9 9"}

    {9}

    Returns: 512

  7. {"9 9", "1 1", "0 1", "2 2", "3 3", "4 4", "5 5", "6 6", "7 7", "8 8"}

    {1}

    Returns: 512

  8. {"0 0 0 0 0 0"}

    {}

    Returns: 1

  9. {"4 4","5 1","4 3","5 1","2 0","4 5"}

    {3,0,4,5,2,1}

    Returns: 1

  10. {"0 2 2 2 2","1 2 2 1 1","0 2 1 0 2"}

    {1}

    Returns: 8

  11. {"1 1 0 0 0 1 1 0 0 2","0 1 1 2 2 1 0 2 1 0","2 1 0 2 1 1 2 1 2 2"}

    {2,1}

    Returns: 8

  12. {"1","2","0"}

    {2,0,1}

    Returns: 1

  13. {"1 2 3 3","0 0 0 3","3 3 1 5","0 1 5 0","3 3 4 2","0 4 1 5"}

    {3,0,4,1}

    Returns: 48

  14. {"2 0 5 1 5 0 4 1 2 4","2 4 4 0 4 0 2 2 4 5","3 0 2 3 3 4 3 1 1 1","4 2 4 1 2 3 1 0 5 5","0 1 4 5 0 5 1 4 3 1","3 2 5 1 5 3 3 0 1 3"}

    {5,4}

    Returns: 58

  15. {"0 0 2 0 1 2 2 1 0 2","0 0 1 3 0 3 2 2 2 2","3 0 2 1 1 1 0 0 0 1","2 3 3 3 2 0 3 2 0 0"}

    {1}

    Returns: 16

  16. {"1 7 7 1 1 2 8","5 4 0 4 3 6 0","0 9 2 2 6 6 1","1 7 3 0 9 6 0","8 6 3 9 1 4 4","8 0 9 0 4 5 9","5 4 2 8 0 4 5","9 1 2 6 4 9 6","2 2 6 8 0 0 8","1 9 4 5 4 2 4"}

    {1,0,4,3,6,5,7}

    Returns: 572

  17. {"0 0 0 0 0 0 0 0 0 0"}

    {}

    Returns: 1

  18. {"3 6 5 2 7 1 2 6 3 5","6 0 7 1 2 5 6 0 5 6","5 7 4 3 3 2 0 2 6 1","5 6 0 1 6 4 3 0 2 3","4 1 1 7 1 2 6 1 5 3","7 3 6 7 4 3 5 5 4 7","2 6 1 0 1 2 1 4 6 5","4 5 2 5 4 3 0 2 4 6"}

    {0,5,4,1,7,2}

    Returns: 228

  19. {"0 1 0 0 0 1 0 3 3 2","3 3 3 1 2 0 2 1 2 1","3 1 0 3 2 1 2 0 2 3","1 3 1 3 2 0 0 1 3 3"}

    {0}

    Returns: 16

  20. {"1 3 2 2 1 6 7 1 3","3 2 2 1 4 2 2 4 5","3 4 4 0 5 2 6 7 5","2 2 6 2 6 4 6 5 6","5 1 4 6 4 5 6 3 0","3 4 3 3 5 6 3 7 5","0 6 4 3 7 2 4 5 2","1 0 6 2 4 1 1 4 6"}

    {3,1,6,4,0,7,2,5}

    Returns: 1

  21. {"3 0 0","5 3 8","6 6 2","6 7 9","9 1 7","5 9 6","5 2 0","0 4 3","5 3 6","9 8 5"}

    {}

    Returns: 1

  22. {"0 0 0 5 0","2 4 5 4 1","4 0 5 6 2","2 5 5 5 6","4 6 0 4 5","0 3 5 3 6","2 2 3 1 4"}

    {4,6}

    Returns: 98

  23. {"8 1 8 3 7","6 0 9 6 5","9 1 5 9 9","4 1 8 8 0","5 6 3 1 0","5 9 9 8 8","7 6 2 9 4","3 7 8 1 3","7 9 0 4 6","5 2 6 9 0"}

    {9,3,4,5,7}

    Returns: 371

  24. {"2 3 3 4 2 5 2 1 4 4","4 4 4 6 2 1 6 6 5 1","5 7 3 0 3 5 3 0 1 5","4 5 7 0 0 7 4 2 1 2","6 1 0 1 3 3 2 6 0 1","3 4 4 2 1 0 0 7 5 3","3 2 3 6 4 5 5 0 1 1","2 7 6 5 2 4 5 6 0 0"}

    {1,6,5,2,0,4,3,7}

    Returns: 1

  25. {"0 0 0 0 1 0 0 0","0 0 1 1 1 1 0 0"}

    {0}

    Returns: 3

  26. {"6 3 5 5 1 6 1 0","1 3 2 8 8 2 5 4","7 3 6 8 7 2 5 7","6 0 3 3 7 0 7 3","6 6 4 5 3 2 0 4","4 0 8 7 5 3 9 6","7 7 3 7 2 4 5 7","7 0 8 3 0 0 5 5","3 0 7 7 9 4 5 1","7 1 9 1 9 6 5 5"}

    {2,4,6,8}

    Returns: 469

  27. {"6 5 7 0 0 4 2","6 0 5 1 3 0 5","3 7 3 5 6 3 1","5 4 7 6 6 3 7","2 4 0 5 4 1 1","4 0 3 0 3 0 6","2 1 4 1 2 7 7","4 3 4 5 7 4 2"}

    {6,7,4,2,3,0,5}

    Returns: 156

  28. {"0 0"}

    {0}

    Returns: 1

  29. {"1 0 5 4 0 1 5 3","7 3 1 4 4 0 6 4","1 4 6 7 5 5 3 6","1 1 0 4 3 4 4 3","3 7 1 2 6 4 1 2","4 4 5 1 3 2 4 4","6 4 3 1 1 3 5 7","1 1 4 6 0 0 4 2"}

    {4,5,3,2,6,7,0,1}

    Returns: 1

  30. {"4 2 2 3","2 4 4 1","5 5 3 2","0 0 4 5","0 4 1 1","4 5 0 2"}

    {}

    Returns: 1

  31. {"1 2 2 2 1","2 0 1 0 0","2 1 2 2 0"}

    {0,1,2}

    Returns: 1

  32. {"4 7 5 0 4 5 3","1 3 7 1 4 5 5","6 6 0 1 9 3 1","6 5 1 3 8 2 4","7 6 1 5 4 2 2","8 8 8 8 8 0 2","1 8 6 7 7 9 2","9 3 6 5 3 3 0","4 9 1 9 4 8 3","7 8 1 0 5 3 3"}

    {0,5,4,7,8,6}

    Returns: 379

  33. {"4 4 1 4 0 3","1 4 2 0 0 4","2 0 4 1 0 3","4 3 0 1 4 0","1 1 3 3 4 4"}

    {1,0,4}

    Returns: 32

  34. {"0 5 5 7 1 2 3 0","5 0 3 1 2 4 5 8","3 9 5 3 9 3 4 6","8 0 4 7 7 3 6 6","4 3 8 8 5 2 5 5","4 6 3 5 2 6 8 4","5 1 4 8 1 8 0 7","9 7 4 8 0 1 8 1","4 3 2 1 6 8 4 6","8 0 0 6 9 3 7 8"}

    {2,9,6,1,0,4,7,5,3}

    Returns: 518

  35. {"1 1 0 0","1 1 1 1"}

    {}

    Returns: 1

  36. {"0 1 0 0 1 1","0 0 0 1 1 1"}

    {}

    Returns: 1

  37. {"1 5 3 6","5 6 1 5","1 1 3 5","1 4 0 2","4 6 2 1","3 4 5 6","5 2 4 2"}

    {0,4,2,3,5,1}

    Returns: 74

  38. {"4 8 9 9 4 9 7 4","6 7 2 7 9 4 9 2","2 1 2 1 5 7 6 6","9 4 5 7 7 7 9 9","3 6 2 1 3 4 1 7","5 2 4 7 8 5 2 1","0 5 4 5 0 0 0 8","1 9 7 1 5 4 7 3","1 3 2 2 6 3 4 6","7 4 2 7 2 5 4 0"}

    {4,6}

    Returns: 1024

  39. {"0 1", "5 2", "3 4", "3 2", "5 4", "5 5"}

    {1,2,3,4}

    Returns: 7

  40. { "0 1", "1 2", "2 3", "3 2" }

    { 0, 2 }

    Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: