Statistics

Problem Statement

A sign test is a test that is performed to determine if the results of an experiment are statistically significant. In particular, it looks at a number of similar trials, where each trial's outcome is either positive or negative. It calculates the probability that the results of your experiments would be at least as unbalanced as they actually turned out to be if the outcomes of each trial were totally random - a 50% chance of being positive and a 50% chance of being negative. For example, the probability of the five trials being split 4-1 or 5-0 is 12/32: 2 out of 32 times the results will be 5 negatives or 5 positives and 10 out of 32 times the results will have 4 negatives or 4 positives. Hence, the p-value of an outcome with 4 positives and 1 negative is 12/32 = 0.375. To make this more concrete, the p-value of N trials, K of which are negative can be calculated as

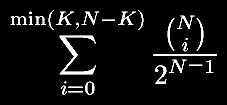
where the numerator of the fraction is the binomial coefficient: N!/(i!(N-i)!). There is one exception to this though: when K*2 is equal to N, the p-value is simply 1 (the above equation gives the wrong result).

This is all quite simple, when N and K are small, but what if they are rather large? Your task is to compute the p-value, given N and K, where 0<=K<=N<=1,000,000 and 0<N. You should return this value as a percentage with exactly one digit after the decimal point (don't forget the percent sign). You should use standard rounding when formatting your return. You need not worry about borderline cases as the constraints ensure that the percentage will not be within 1e-3 of XX.X5, where each X represents a digit.

Definition

Class:

LargeSignTest

Method:

pvalue

Parameters:

int, int

Returns:

String

Method signature:

String pvalue(int N, int K)

(be sure your method is public)

Constraints

• N will be between 1 and 1,000,000, inclusive.
• K will be between 0 and N, inclusive.
• The percentage will not be within 1e-3 of XX.X5, where each X represents a digit.

Examples

1. 5

   4

   Returns: "37.5%"

   The p-value in this case is (choose(5,0)+choose(5,1))/2N-1 = (1+5)/16 = 6/16 = 3/8 = 37.5%

2. 10

   5

   Returns: "100.0%"

3. 1000000

   400000

   Returns: "0.0%"

4. 20

   5

   Returns: "4.1%"

5. 1000000

   499000

   Returns: "4.6%"

6. 1000

   499

   Returns: "97.5%"

7. 1000000

   499900

   Returns: "84.2%"

8. 457751

   229032

   Returns: "64.5%"

9. 954446

   479806

   Returns: "0.0%"

10. 502911

    249637

    Returns: "0.0%"

11. 162292

    80431

    Returns: "0.0%"

12. 479035

    238355

    Returns: "0.1%"

13. 292167

    146597

    Returns: "5.8%"

14. 722324

    364093

    Returns: "0.0%"

15. 300832

    149379

    Returns: "0.0%"

16. 986163

    495307

    Returns: "0.0%"

17. 212614

    106655

    Returns: "13.2%"

18. 499735

    250759

    Returns: "1.2%"

19. 465049

    230910

    Returns: "0.0%"

20. 62707

    31714

    Returns: "0.4%"

21. 426743

    212838

    Returns: "10.3%"

22. 355025

    177343

    Returns: "57.1%"

23. 512663

    258013

    Returns: "0.0%"

24. 504064

    252709

    Returns: "5.7%"

25. 732662

    367636

    Returns: "0.2%"

26. 630450

    316450

    Returns: "0.2%"

27. 513709

    255519

    Returns: "0.0%"

28. 449366

    226714

    Returns: "0.0%"

29. 627692

    314911

    Returns: "0.7%"

30. 170104

    84908

    Returns: "48.7%"

31. 570838

    284285

    Returns: "0.3%"

32. 197878

    98774

    Returns: "46.0%"

33. 506653

    252639

    Returns: "5.4%"

34. 333151

    165058

    Returns: "0.0%"

35. 79293

    39398

    Returns: "7.8%"

36. 669425

    335217

    Returns: "21.8%"

37. 605891

    300970

    Returns: "0.0%"

38. 943172

    469649

    Returns: "0.0%"

39. 865111

    429194

    Returns: "0.0%"

40. 667554

    334721

    Returns: "2.1%"

41. 882406

    438049

    Returns: "0.0%"

42. 974458

    491148

    Returns: "0.0%"

43. 129036

    64181

    Returns: "6.1%"

44. 716422

    359057

    Returns: "4.6%"

45. 560756

    279169

    Returns: "0.1%"

46. 610338

    307010

    Returns: "0.0%"

47. 972259

    489086

    Returns: "0.0%"

48. 68449

    34080

    Returns: "27.1%"

49. 750374

    375915

    Returns: "9.3%"

50. 486053

    241545

    Returns: "0.0%"

51. 684392

    344465

    Returns: "0.0%"

52. 731670

    368413

    Returns: "0.0%"

53. 768859

    382409

    Returns: "0.0%"

54. 76081

    37952

    Returns: "52.3%"

55. 892301

    447204

    Returns: "2.6%"

56. 123559

    61668

    Returns: "52.8%"

57. 815121

    405574

    Returns: "0.0%"

58. 1000000

    499999

    Returns: "99.9%"

59. 1000000

    499996

    Returns: "99.4%"

60. 1000000

    499000

    Returns: "4.6%"

61. 5

    4

    Returns: "37.5%"

62. 1000000

    499997

    Returns: "99.6%"

63. 1000000

    499980

    Returns: "96.9%"

64. 1000000

    499995

    Returns: "99.3%"

65. 2

    0

    Returns: "50.0%"

66. 1000000

    499900

    Returns: "84.2%"

67. 1000000

    500001

    Returns: "99.9%"

68. 1000000

    499599

    Returns: "42.3%"

69. 1

    0

    Returns: "100.0%"

70. 1000

    497

    Returns: "87.4%"

71. 1000000

    200000

    Returns: "0.0%"

72. 1000000

    499700

    Returns: "54.9%"

73. 1000

    495

    Returns: "77.6%"

74. 202

    100

    Returns: "94.4%"

75. 999999

    499999

    Returns: "100.0%"

76. 1000000

    498262

    Returns: "0.1%"

77. 81

    40

    Returns: "100.0%"

78. 1001

    459

    Returns: "1.0%"