Statistics

Problem Statement for "DiscCover"

Problem Statement

We are given a disc of radius discRadius and want to cover it using numDiscs small discs - i.e., place the small discs flat above the original disc in such a way that no point of the original disc is visible (assuming the small discs are opaque). All smaller discs we use for the covering have the same radius.

We perform the covering using the following procedure:

  1. In the first step, we split the disc into several rings using concentric circles (with the same center as the original disc). Note that the innermost "ring" will have an inner radius 0, and thus will actually be a disc. We are free to split the disc into as many rings and at whatever positions we want (i.e., use circles of arbitrary radii). The example below shows a disc split into three rings (blue, green and red).
  2. In the second step, we regard each of the rings independently, and try to cover each of them using some number of the small discs. We can either use one small disc, which has to be centered at the center of the original disc, or use three or more discs, whose centers must be the vertices of a regular polygon centered at the center of the original disc. The example below shows one such case: The innermost ring (red, actually a disc) is covered by one small disc (which has the same radius as the red disc), the green ring is covered by 6 small discs centered at the vertices of a regular hexagon around the center, and the outermost blue ring is covered by 12 small discs centered at the vertices of a regular 12-gon. Please note that we try to cover each ring totally independently of the others, i.e., ignore that parts in one ring may have been covered already by the discs used to cover another ring (in the example below, the discs used to cover the green ring would also cover parts of the blue and red rings, but we ignore this fact).

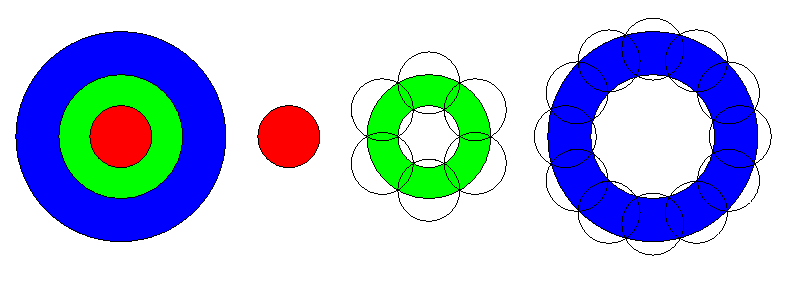
In summary, we have the freedom to choose the number and size of the rings that the original disc is split into, how many of the numDiscs discs are used for covering each of the rings, and the distance from the center at which the small discs for each ring are placed. We will have to choose these parameters such that a covering using this procedure is possible using the smallest possible discs.

Given discRadius, the radius of the original disc, and numDiscs, the total number of small discs to use, return the minimum radius that the small discs must have so that a covering using the above procedure is possible.

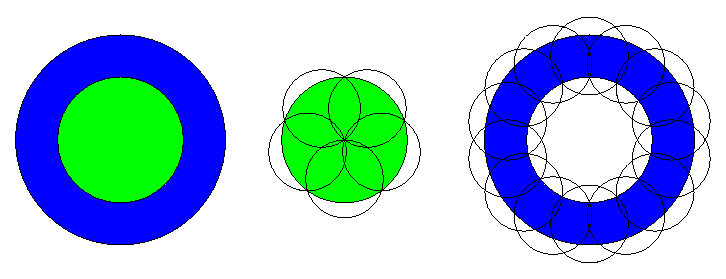
The example shown above is only one possibility to cover the original disc using 19 small discs (which turns out to be the optimal one for the used procedure). The figure below shows as an example another (non-optimal) possibility: here, the original disc is split only into two rings, and 5 of the small discs are used to cover the inner (green) ring, the other 14 small discs are used to cover the outer (blue) ring. It is clear here that too much space is wasted in the outer ring (that ring was chosen too narrow), so this can not be an optimal solution.

Definition

Class:
DiscCover
Method:
minRadius
Parameters:
double, int
Returns:
double
Method signature:
double minRadius(double discRadius, int numDiscs)
(be sure your method is public)

Notes

  • When covering one ring with small discs, we ignore that there are parts of this ring covered already by the discs used for other rings.
  • The innermost "ring" will be a disc (i.e. the inner radius will be 0).
  • There may be just one "ring" in total (i.e. all smaller discs build a single regular polygon around the center).
  • Your return value must have an absolute or relative error less than 1e-9.

Constraints

  • discRadius is between 1.0 and 1000.0, inclusive.
  • numDiscs is between 1 and 2000, inclusive.

Examples

  1. 1000.0

    1

    Returns: 1000.0

    Here we can use only one disc to cover the given one. This must be at least as large as the original one.

  2. 500.0

    2

    Returns: 500.0

    Using a second disc doesn't help much.

  3. 100.0

    3

    Returns: 86.60254037844385

    Three discs of radius r placed in a triangle configuration around the center can cover a disc of maximum radius 2 * r / sqrt(3) (the centers of the small discs must be placed in a distance of 2 * r / 3 from the centers to achieve this maximum). So, to cover a disc of radius discRadius, we need three discs of radius discRadius * sqrt(3) / 2. This optimum is shown in the figure below:

  4. 100.0

    4

    Returns: 70.71067811865474

    This is the traditional game that can be found in some amusement parks, where you have to cover a disc using four smaller ones. The small discs must be at least 0.707 ( = sqrt(2)/2 ) times smaller than the disc to cover. The optimal configuration is shown below:

  5. 200.0

    19

    Returns: 59.085199376486976

    The example from the problem statement. The first configuration given in the problem statement is the optimal one for 19 discs.

  6. 779.7195729322183

    5

    Returns: 481.8931977656634

  7. 375.46046174484934

    6

    Returns: 216.77219865844995

  8. 479.2373090258489

    7

    Returns: 239.6186545129244

  9. 586.6805039604749

    13

    Returns: 214.73996835459076

  10. 876.2866593398353

    14

    Returns: 306.93209303976926

  11. 109.67261886931746

    15

    Returns: 37.097993060663235

  12. 836.8033590847328

    999

    Returns: 33.20125265058916

  13. 12.752403667008178

    1000

    Returns: 0.5057147194116579

  14. 310.3259583138488

    1999

    Returns: 8.703865181119534

  15. 484.9357709515974

    2000

    Returns: 13.597909402292117

  16. 690.2220812433532

    862

    Returns: 29.485376958886214

  17. 459.89846273181126

    731

    Returns: 21.348063571945172

  18. 5.772714384852982

    496

    Returns: 0.32523065072085294

  19. 187.17302728004987

    299

    Returns: 13.584523147514927

  20. 903.4631286386987

    873

    Returns: 38.34739017469602

  21. 237.09681188630594

    158

    Returns: 23.74452181493388

  22. 58.226310880831534

    256

    Returns: 4.571245517861806

  23. 824.3152024715887

    69

    Returns: 124.72775945454421

  24. 398.90959109528546

    236

    Returns: 32.59584821652047

  25. 777.0894550612827

    982

    Returns: 31.097348093727163

  26. 617.2074217953603

    861

    Returns: 26.381957066442947

  27. 566.1923417415106

    271

    Returns: 43.250908831662535

  28. 426.3789580476775

    498

    Returns: 23.97189941357355

  29. 293.6822513466168

    971

    Returns: 11.819609444976326

  30. 965.2853566888642

    860

    Returns: 41.284827800335975

  31. 907.6719248658185

    53

    Returns: 158.49640480707095

  32. 292.4129706429005

    207

    Returns: 25.56652959919992

  33. 415.4031176113544

    214

    Returns: 35.7520412325665

  34. 850.0311467181792

    530

    Returns: 46.328107768174085

  35. 23.419362938968668

    574

    Returns: 1.2264972402771284

  36. 636.9049822024917

    90

    Returns: 84.85292273419951

  37. 970.5351414096776

    654

    Returns: 47.617524155797035

  38. 277.45066340855914

    864

    Returns: 11.83831507607381

  39. 562.7339630204957

    343

    Returns: 38.152628780622045

  40. 314.81903764985856

    176

    Returns: 29.830092953301047

  41. 97.83625245786688

    86

    Returns: 13.352856789813641

  42. 448.06512088210746

    272

    Returns: 34.156521926705786

  43. 867.2727698198886

    407

    Returns: 53.98236644079314

  44. 484.27781429445565

    764

    Returns: 21.97527026384189

  45. 255.85831953934516

    716

    Returns: 11.997121659639499

  46. 723.5263905746866

    184

    Returns: 66.97815979500122

  47. 915.0466647239282

    933

    Returns: 37.58829882359304

  48. 428.0402110769452

    54

    Returns: 74.1286183092835

  49. 363.77574049771533

    268

    Returns: 27.954012809104302

  50. 198.029837967797

    281

    Returns: 14.838089447685343

  51. 628.145398547077

    1234

    Returns: 22.42216998317222

  52. 867.6492641636559

    1605

    Returns: 27.154732965147975

  53. 992.7379464408599

    1207

    Returns: 35.831557456669394

  54. 467.6827224454546

    1726

    Returns: 14.115645653919328

  55. 152.59410532914546

    1694

    Returns: 4.649645784103721

  56. 550.2971310534449

    1523

    Returns: 17.68160516083071

  57. 625.3825478462569

    1728

    Returns: 18.864317791053544

  58. 987.4576971111999

    1632

    Returns: 30.647012994778663

  59. 889.6986137249943

    1398

    Returns: 29.84083509495132

  60. 235.29639894714958

    1792

    Returns: 6.968988944925376

  61. 286.33323394092696

    1406

    Returns: 9.576993092713032

  62. 358.4264399020529

    1521

    Returns: 11.524059526188287

  63. 674.8501884489827

    1236

    Returns: 24.069872850346236

  64. 1.0

    2000

    Returns: 0.028040640053441958

  65. 1000.0

    2000

    Returns: 28.040640053441958

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: