Problem Statement
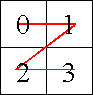
Here is a diagram of a Z-curve of order 2.
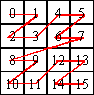
Notice the order each quadrant was visited:
- upper left quadrant: 0, 1, 2, 3
- upper right quadrant: 4, 5, 6, 7
- lower left quadrant: 8, 9, 10, 11
- lower right quadrant: 12, 13, 14, 15
You will be given a value N and coordinates r and c denoting the row and the column in a 2^N by 2^N grid. Coordinates range from 0 to (2^N)-1 inclusive, with the upper left corner at coordinates (0,0). Assuming you start from the upper left corner and the points are traversed in the order specified by a Z-curve of order N, determine how many steps it takes to reach the point at coordinates (r,c).
Definition
- Class:
- ZCurve
- Method:
- zValue
- Parameters:
- int, int, int
- Returns:
- int
- Method signature:
- int zValue(int N, int r, int c)
- (be sure your method is public)
Constraints
- N is between 1 and 15, inclusive.
- r and c are between 0 and 2^N-1, inclusive.
Examples
2
3
1
Returns: 11
1
0
0
Returns: 0
3
7
7
Returns: 63
(7,7) is in the lower right corner of the grid and, as shown in the following diagram, it is the last point visited.
4
7
7
Returns: 63
The upper left quadrant of a Z-curve of order 4 is actually a Z-curve of order 3 and, because it is the first quadrant visited, the answer is the same as in the previous example.
10
511
511
Returns: 262143
10
512
512
Returns: 786432
1
0
1
Returns: 1
15
32157
32212
Returns: 1072944050
15
24224
2
Returns: 581470212
14
4095
4094
Returns: 16777214
13
4094
4095
Returns: 16777213
1
1
1
Returns: 3
1
1
0
Returns: 2
15
27207
2764
Returns: 684486778
15
2937
5651
Returns: 27143047
15
21630
16852
Returns: 841055160
15
4753
8866
Returns: 101500422
15
2764
24778
Returns: 344518884
15
15244
25405
Returns: 512722417
15
7971
32445
Returns: 402541915
7
37
110
Returns: 7286
15
7613
16885
Returns: 312729523
14
6185
13535
Returns: 126900695
15
4990
19020
Returns: 307116792
11
1456
35
Returns: 2264581
3
6
0
Returns: 40
15
454
17476
Returns: 269660216
15
21909
26593
Returns: 909628963
15
32119
29
Returns: 715271035
15
15101
19012
Returns: 449624754
15
29819
3285
Returns: 712014747
10
619
226
Returns: 556174
11
1522
1836
Returns: 3649112
15
4266
7215
Returns: 55610589
15
23791
32081
Returns: 938588587
15
28445
12136
Returns: 754915042
15
24527
23664
Returns: 872068522
3
6
5
Returns: 57
15
11903
25932
Returns: 481901306
8
63
37
Returns: 3771
3
7
1
Returns: 43
2
2
1
Returns: 9
7
48
105
Returns: 7745
15
26488
29080
Returns: 1026255808
2
0
1
Returns: 1
15
19354
25111
Returns: 881755037
6
23
27
Returns: 879
15
1371
13940
Returns: 87439258
11
18
326
Returns: 70172
15
22834
26276
Returns: 915820056
7
6
25
Returns: 361
14
15752
4428
Returns: 195268816
11
1701
443
Returns: 2739559
14
480
16350
Returns: 89651540
8
57
224
Returns: 24194
15
32515
21379
Returns: 1001340943
15
18091
6438
Returns: 560565406
15
4252
14801
Returns: 121754529
15
29632
12398
Returns: 789230676
15
21204
22899
Returns: 860469029
15
21811
1926
Returns: 574048798
15
32452
1617
Returns: 717009185
3
7
4
Returns: 58
15
22239
2524
Returns: 577369082
15
1757
23342
Returns: 292398838
15
28827
14213
Returns: 789955227
15
32260
22139
Returns: 1002181989
15
6917
28302
Returns: 383664246
15
32228
24222
Returns: 1006037364
15
14853
25011
Returns: 512312615
11
856
1683
Returns: 1991557
14
15483
4698
Returns: 195312590
15
1896
2208
Returns: 6974592
15
26495
12365
Returns: 757742331
15
18377
13400
Returns: 624603586
3
1
5
Returns: 19
12
1024
679
Returns: 2376725
15
32767
32767
Returns: 1073741823
1
0
0
Returns: 0
3
7
7
Returns: 63
10
511
511
Returns: 262143
15
32766
32767
Returns: 1073741821
8
13
7
Returns: 183
10
512
512
Returns: 786432
15
32767
32767
Returns: 1073741823
15
15
32767
Returns: 357914111
13
213
17
Returns: 41763
15
32719
32719
Returns: 1073737983
15
16
7
Returns: 533
15
31581
31581
Returns: 1070543859
2
0
2
Returns: 4
6
8
9
Returns: 193
3
5
6
Returns: 54
15
32761
32651
Returns: 1073736391
1
1
0
Returns: 2
13
20
25
Returns: 865
15
32767
32765
Returns: 1073741819
1
1
1
Returns: 3
15
30000
30000
Returns: 1060310784
2
0
3
Returns: 5
2
1
0
Returns: 2
2
2
3
Returns: 13