Problem Statement
You have decided to put new floor tiles on your bedroom floor. Consider an infinite pattern made of 1x5 wooden panels as in the picture below. The top-left corner of the picture has coordinates (0, 0). X coordinates increase from left to right, and y coordinates increase from top to bottom.
You have chosen a rectangular area within this infinite pattern that matches the exact size of your bedroom. The top-left corner of the rectangle is at (x1, y1) and the bottom-right corner is at (x2, y2). You want to reproduce this section on your bedroom floor.
The store that sells wooden floor panels only carries 1x5 panels. You can cut panels to get smaller panels, but you can't glue panels together to get larger ones. For example, you can cut a 1x5 panel to get one 1x3 panel and one 1x2 panel, or two 1x2 panel and one 1x1 panel, etc.
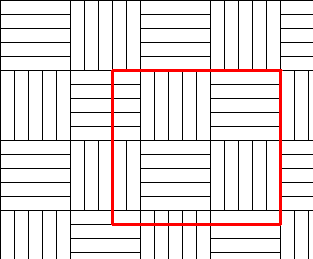
The picture above shows the rectangular area (8, 5, 20, 16). You need twenty-three 1x5 panels, six 1x2 panels and five 1x1 panels. You have to buy total of 27 panels to make these.
You are given ints x1, y1, x2 and y2. Return the minimum number of panels you must buy at the store to produce the pattern in the given rectangular area.
Definition
- Class:
- BedroomFloor
- Method:
- numberOfSticks
- Parameters:
- int, int, int, int
- Returns:
- long
- Method signature:
- long numberOfSticks(int x1, int y1, int x2, int y2)
- (be sure your method is public)
Notes
- You can throw away any part of a panel that you don't need.
Constraints
- x1, y1, x2 and x2 will be between 0 and 1000000, inclusive.
- x2 will be strictly greater than x1.
- y2 will be strictly greater than y1.
Examples
0
0
5
5
Returns: 5
This rectangular area contains five 1x5 panels.
0
0
10
2
Returns: 5
This rectangular area contains two 1x5 panels and five 1x2 panels. We have to buy 5 panels to make these.
2
2
8
8
Returns: 12
This rectangle contains twelve 1x3 panels. We can't glue panels together, so we have to buy 12 panels.
8
5
20
16
Returns: 27
The example depicted in the problem statement.
0
0
1000000
1000000
Returns: 200000000000
9
3
10
9
Returns: 2
101
102
203
204
Returns: 2142
1
1
2
2
Returns: 1
12
37
89
83
Returns: 753
49
51
64
70
Returns: 58
32
2
75
31
Returns: 259
68
21
78
94
Returns: 148
73
36
74
97
Returns: 13
10
82
15
91
Returns: 9
80
83
87
88
Returns: 7
42
34
67
80
Returns: 230
66
79
68
98
Returns: 9
27
56
74
69
Returns: 136
58
85
62
86
Returns: 1
17
2
21
66
Returns: 58
42
91
91
95
Returns: 45
24
23
77
88
Returns: 689
71
15
75
76
Returns: 54
26
44
49
48
Returns: 21
36
77
75
81
Returns: 36
24
7
26
60
Returns: 22
53
26
62
41
Returns: 28
36
59
79
83
Returns: 216
0
39
64
64
Returns: 322
19
79
64
82
Returns: 27
615446
163644
749490
650135
Returns: 13042275165
321707
271981
634146
453664
Returns: 11353051623
94514
373398
504724
692624
Returns: 26190001024
532129
292948
654675
356541
Returns: 1558613556
270876
199737
749362
878413
Returns: 64947516434
334703
463001
849526
939461
Returns: 49058513316
177768
453617
938416
956955
Returns: 76572609734
851663
776821
888567
943688
Returns: 1231630486
825156
475253
948036
598772
Returns: 3035615232
339763
786347
433350
978569
Returns: 3597910353
168821
456163
844707
936819
Returns: 64973905725
759046
16775
992749
710361
Returns: 32418741139
970271
859014
998515
877826
Returns: 106265226
553328
159457
696612
382583
Returns: 6394085141
615868
774738
823539
865654
Returns: 3776168115
180432
231705
746417
928042
Returns: 78823287689
535905
131492
895196
915257
Returns: 56319942123
620673
50521
700563
431891
Returns: 6093529860
819262
401220
939252
726504
Returns: 7806177431
245975
47960
471041
855069
Returns: 36330558839
319836
198500
832177
903900
Returns: 72281174090
446945
123155
830881
924441
Returns: 61528508340
169374
473311
373539
499159
Returns: 1055492217
520038
828436
527848
907168
Returns: 122981727
400514
924669
719526
953442
Returns: 1835786456
2282
18669
462561
118692
Returns: 9207697284
189023
53547
889895
398667
Returns: 48377006184
259624
740923
265248
920593
Returns: 202110783
363687
865797
511521
877930
Returns: 358764765
581910
771045
763835
961963
Returns: 6946587814
170148
981582
961220
984368
Returns: 441101190
646630
343131
696966
512509
Returns: 1705162202
575419
501044
734755
960723
Returns: 14648682629
945345
57113
977501
837110
Returns: 5016316707
917486
610702
952849
914047
Returns: 2145498517
177100
867939
220713
949260
Returns: 709342457
224275
789663
654529
840762
Returns: 4397157965
361188
394953
946983
501011
Returns: 12425649222
426976
12306
757402
637240
Returns: 41299015160
476643
819298
816047
885033
Returns: 4462150962
76315
202130
728241
892697
Returns: 90039716409
811965
37600
861948
837565
Returns: 7997090111
689047
229317
861501
830793
Returns: 20745517550
580150
266661
824902
645306
Returns: 18534843140
272094
274291
590527
581202
Returns: 19546150512
341095
856415
783791
944642
Returns: 7811561311
612593
765276
614601
809232
Returns: 17652730
132678
77197
961955
125990
Returns: 8092738629
121098
82827
426303
595423
Returns: 31289494518
0
0
1
1000000
Returns: 200000
0
0
1000000
1
Returns: 200000
9
12
51
55
Returns: 362
32
53
57
85
Returns: 161
23
40
65
64
Returns: 207
39
42
45
89
Returns: 57
3
63
30
76
Returns: 71
9
4
94
42
Returns: 646
9
4
34
52
Returns: 240
19
11
40
52
Returns: 173
2
3
999777
999777
Returns: 199909910148
7
17
999987
999982
Returns: 199989000140
1
6
999998
999992
Returns: 199996800007
7
8
999996
999999
Returns: 199996000020
8
2
999999
999996
Returns: 199997000011
4353
4568
34567
56778
Returns: 315499809
2
1
999473
999982
Returns: 199890702056
77
79
98721
97148
Returns: 1915074458
8
4
999993
999997
Returns: 199995600021
2
1
999997
999996
Returns: 199998000006
2
2
4
4
Returns: 1
19
4126
987642
874231
Returns: 171867142083
3
9
11
13
Returns: 7
2
8
999997
999924
Returns: 199982350083
81
93
99871
97971
Returns: 1953449124
1
2
4
500003
Returns: 400001
1
1
3
3
Returns: 1
4
0
14
5
Returns: 10
2
0
7
1
Returns: 1
0
0
300013
300006
Returns: 18001170016
1
2
999987
999986
Returns: 199994000045
1
1
4
4
Returns: 3
6
1
17
7
Returns: 16
2
2
3
3
Returns: 1
2
0
999991
999991
Returns: 199996000020
1
1
4
999999
Returns: 799999
1
0
6
1
Returns: 1
1
1
2
3
Returns: 1
13
12
60
26
Returns: 134
1
2
999998
999996
Returns: 199998600001
3
3
14
4
Returns: 3
2
0
7
8
Returns: 10
5
4
8
6
Returns: 2
4
5
46
22
Returns: 143
3
0
8
1
Returns: 1
0
1
4
6
Returns: 4
3
0
6
1
Returns: 1
0
3
1
8
Returns: 1
2
0
11
5
Returns: 10
9
2
13
6
Returns: 4