Problem Statement
We are in a Manhattan-type city with north-south directed avenues labeled "A" to "Z" and east-west directed streets numbered 1 to 50. A crossing is represented by the label of the avenue followed by the label of the street defining that crossing, with no leading zeros (e.g., the crossing between avenue "D" and street number 12 is represented as "D12").
The figure below shows part of the city (avenues E to G, streets 2 to 4). The distance between neighboring streets and between neighboring avenues will be the same for all pairs of neighboring avenues or streets, and will be given by the input parameter distance (in meters). This distance is measured from the center of the streets or avenues, as shown in the figure. Further, all streets and avenues will have the same width, which will be given by the input parameter width (also in meters), as shown in the figure.
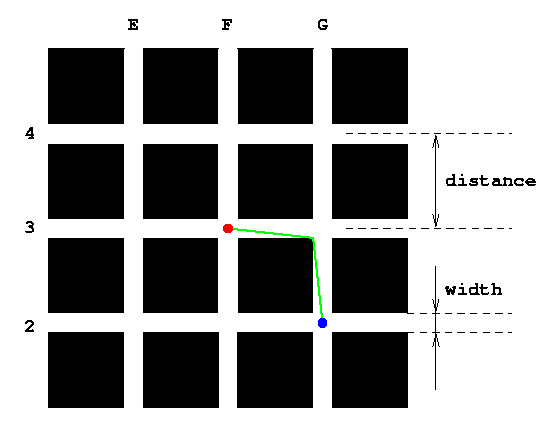
Given distance and width as defined above, as well as the representation of two crossings, start and target (formatted as described above), return the minimum distance you have to travel (in meters) beginning from the center of the crossing start to reach the center of the crossing target if you are only allowed to travel on streets and avenues. For example, if start is "F3" (the red dot in the figure above) and target is "G2" (the blue dot), the green line shows one possible optimal path to go from start to target (another optimal path with the same length would be to go first south to the north-east corner of crossing "F2" and then to the east to our target).
Definition
- Class:
- ManhattanDistance
- Method:
- minDistance
- Parameters:
- int, int, String, String
- Returns:
- double
- Method signature:
- double minDistance(int distance, int width, String start, String target)
- (be sure your method is public)
Notes
- Your return value must have an absolute or relative error less than 1e-9.
Constraints
- distance will be between 2 and 1000, inclusive.
- width will be between 1 and 500, inclusive.
- width will be no greater than half of distance.
- start and target will be formatted as "
" (quotes for clarity), where will be an uppercase letter ('A' - 'Z') and will be an integer between 1 and 50, inclusive, with no leading zeros.
Examples
100
10
"B1"
"B4"
Returns: 300.0
Both start and target are at the same avenue ('B'), so just go along the center of this avenue 3 blocks (each of them 100 meters long).
100
20
"F3"
"G2"
Returns: 181.10770276274835
The example from the problem statement. An optimal path is shown by the green line in the figure in the problem statement. For the given values distance = 100 and width = 20, each of the two green segments has a length of sqrt(902 + 102) = 90.55385 meters, which gives a total of 181.1077 meters.
1000
1
"E18"
"P9"
Returns: 19982.008508256098
For the case of such narrow streets, the optimal path is not much better than going along the center of the streets (which would be 20000.0 meters).
8
4
"B10"
"E13"
Returns: 35.27652763864304
120
30
"C2"
"D48"
Returns: 5584.950296406279
750
120
"R13"
"R13"
Returns: 0.0
1000
100
"A1"
"Z50"
Returns: 69207.11557621435
1000
10
"A50"
"Z1"
Returns: 73501.91610908862
1000
400
"Z50"
"A1"
Returns: 58330.68063834228
800
100
"C32"
"Y10"
Returns: 31201.81444767227
2
1
"H30"
"G32"
Returns: 4.576491222541475
99
33
"X50"
"G49"
Returns: 1724.1214018374471
1000
1
"Q1"
"Q50"
Returns: 49000.0
900
400
"Z42"
"A42"
Returns: 22500.0
555
42
"G5"
"P1"
Returns: 6888.885625199891
467
58
"P22"
"L26"
Returns: 3356.469988244541
272
8
"L29"
"Y45"
Returns: 7682.966333576751
759
334
"I31"
"Y24"
Returns: 13877.80075181118
195
16
"Q47"
"E29"
Returns: 5480.898437733431
596
5
"H32"
"N45"
Returns: 11264.186565440377
799
199
"A38"
"R10"
Returns: 30083.127280259974
771
221
"T17"
"U45"
Returns: 21960.883123372972
647
12
"F50"
"J24"
Returns: 19314.522591544606
415
132
"J8"
"T38"
Returns: 14331.939957484847
818
309
"U4"
"E44"
Returns: 37764.367305646316
273
13
"U8"
"Y48"
Returns: 11909.423589715932
121
43
"N1"
"S17"
Returns: 2179.9329127395886
752
97
"V13"
"B32"
Returns: 25909.648767696297
40
3
"Q30"
"U15"
Returns: 736.6101241784766
241
1
"U13"
"O14"
Returns: 1685.002429345011
514
247
"E48"
"Q6"
Returns: 23229.514669171138
183
28
"R5"
"D15"
Returns: 3876.770800234099
252
10
"M23"
"P35"
Returns: 3720.769867168054
851
299
"U24"
"U24"
Returns: 0.0
675
236
"Z14"
"F45"
Returns: 26979.98241654982
472
220
"B22"
"S11"
Returns: 9892.453947334456
378
155
"C12"
"X9"
Returns: 8302.296716584588
192
57
"T47"
"N42"
Returns: 1650.7915877787095
826
322
"A17"
"W7"
Returns: 21288.019593736564
214
55
"S9"
"Q32"
Returns: 5149.74734008027
403
151
"H46"
"G23"
Returns: 9413.02981598612
63
20
"J1"
"U11"
Returns: 1008.9191257861272
113
26
"P47"
"E8"
Returns: 5129.968023189821
558
136
"Q50"
"E28"
Returns: 16101.145368072841
521
103
"N8"
"G10"
Returns: 4308.310978428753
458
85
"L21"
"P33"
Returns: 6697.849447392926
96
40
"V2"
"K12"
Returns: 1464.7285022255876
986
336
"L40"
"X10"
Returns: 34662.02053208826
70
14
"K2"
"F33"
Returns: 2389.788462037948
307
62
"V29"
"S15"
Returns: 4874.425198477547
704
175
"U50"
"Z20"
Returns: 23049.873964975322
921
306
"Q2"
"Z21"
Returns: 21187.74533744986
826
240
"I47"
"C41"
Returns: 7764.675870778954
171
8
"J19"
"U37"
Returns: 4786.613576563116
864
289
"U12"
"T33"
Returns: 18500.885965256486
11
5
"V22"
"I46"
Returns: 312.07424175196263
856
339
"G9"
"N40"
Returns: 28608.55889240921
645
66
"S14"
"B33"
Returns: 21099.540796409943
607
241
"E14"
"W29"
Returns: 14839.153479536184
204
102
"J26"
"F21"
Returns: 1332.3008048715647
378
176
"E6"
"X9"
Returns: 7478.79697530916
491
44
"X17"
"K4"
Returns: 11718.879281220667
810
169
"S7"
"G13"
Returns: 12742.277378749617
559
210
"J44"
"Z19"
Returns: 17755.827982560648
697
55
"R32"
"Z24"
Returns: 10361.05166748643
100
1
"A1"
"Z13"
Returns: 3676.0899147673745
1000
500
"A1"
"D50"
Returns: 49645.019201320465
100
20
"F3"
"G2"
Returns: 181.10770276274835
1000
500
"A50"
"Z24"
Returns: 36229.37110822501
121
39
"C2"
"X47"
Returns: 6606.680462291629
1000
3
"A3"
"Z49"
Returns: 70850.1782133365
8
4
"B10"
"E13"
Returns: 35.27652763864304
917
317
"Z7"
"A49"
Returns: 48739.62248628961
120
40
"A7"
"F49"
Returns: 5291.358952474308
213
89
"A3"
"F32"
Returns: 6512.522419441073
1000
1
"A1"
"Z50"
Returns: 73950.01901601092
1000
500
"A1"
"Z50"
Returns: 56332.108232870785
100
50
"C5"
"Z9"
Returns: 2392.416121959579