Statistics

Problem Statement for "VectorPolygon"

Problem Statement

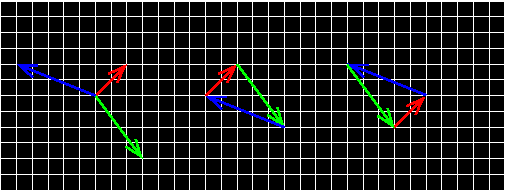
You will be given some two-dimensional vectors (the i-th element of the int[]s dx and dy represent the i-th vector (dx[i], dy[i])). Using some (or all) of these in some order you may be able to construct a polygon by appending them end to end - i.e., represent each vector as an arrow, and place the arrows such that each arrow begins where the last one ends. In order to get a polygon, the last arrow must end at the beginning of the first arrow. The image below shows an example with three vectors.

The left image shows the three vectors as arrows. We can start with the red vector (2, 2), append the green vector (3, -4) and finally append the blue vector (-5, 2) and we get the triangle in the middle image. We can also append them in a different order, starting again with the red one, but appending first the blue one and finally the green one, getting the triangle in the right image.

You are to find the convex polygon that you can construct using some (or all) of the given vectors in some order that has the maximum area, and return this area. If you cannot construct a convex polygon using the given vectors, return 0.0.

Definition

Class:
VectorPolygon
Method:
maxArea
Parameters:
int[], int[]
Returns:
double
Method signature:
double maxArea(int[] dx, int[] dy)
(be sure your method is public)

Notes

  • Your return value must have an absolute or relative error less than 1e-9.
  • If two or more parallel (or even identical) vectors are given in the input, you are allowed to use them in a row - i.e., the polygon may have 180 degrees angles, see example 6.

Constraints

  • dx and dy will each have between 1 and 8 elements, inclusive.
  • dx and dy will have the same number of elements.
  • Each element of dx and dy will be between -100 and 100, inclusive.
  • There will be no zero-vector given, i.e., dx[i] and dy[i] will not be both 0 for any i.

Examples

  1. {2, 3, -5}

    {2, -4, 2}

    Returns: 7.0

    The example from the problem statement. Both shown triangles have the same area.

  2. {2, -3, -5}

    {2, 4, 2}

    Returns: 0.0

    Note that the vectors are directed: this is a similar example as that of the problem statement, but with the green arrow pointing in the opposite direction. We can not construct a polygon using these vectors.

  3. {0, 0, 1, -1}

    {1, -1, 0, 0}

    Returns: 1.0

    We can build a unit square using these four unit vectors.

  4. {25, 50, 75, 100, -25, -50, -75, -100}

    {100, 75, 50, 25, -100, -75, -50, -25}

    Returns: 31250.0

  5. {100}

    {-100}

    Returns: 0.0

  6. {1, -1, 0}

    {0, 1, -1}

    Returns: 0.5

  7. {1,-1}

    {-1,1}

    Returns: 0.0

  8. {1,1,-1,-1}

    {0,0,1,-1}

    Returns: 1.0

  9. {0,1,-1,2,-2}

    {2,-1,-1,-1,-1}

    Returns: 2.0

  10. {0,1,-1,2,-2}

    {2,-1,-1,1,1}

    Returns: 3.0

  11. {100,100,-100,-100}

    {100,-100,100,-100}

    Returns: 20000.0

  12. {0,100,100,100,0,-100,-100,-100}

    {100,100,0,-100,-100,-100,0,100}

    Returns: 70000.0

  13. {0,70,100,70,0,-70,-100,-70}

    {100,70,0,-70,-100,-70,0,70}

    Returns: 47800.0

  14. {10,10,10,10,10,10,10,-70}

    {0,1,2,3,4,5,6,-21}

    Returns: 280.0

  15. {99,-49,-50}

    {100,-50,-50}

    Returns: 25.0

  16. {100,100,-100,-100,0,0,0,0}

    {0,0,0,0,100,100,-100,-100}

    Returns: 40000.0

  17. {10,-10,0,0,-5,-5}

    {0,0,-10,10,21,-21}

    Returns: 205.0

  18. {16,58,-74}

    {94,6,-100}

    Returns: 2678.0

  19. {7,-7}

    {-5,5}

    Returns: 0.0

  20. {20,6,23,-49}

    {-78,57,86,-65}

    Returns: 2958.5

  21. {60,-1,-16,-43}

    {-12,9,-66,69}

    Returns: 2235.0

  22. {14,-14}

    {84,-84}

    Returns: 0.0

  23. {62,-62}

    {96,-96}

    Returns: 0.0

  24. {-51,-63,30,-29,35,78}

    {97,-49,66,-65,-63,14}

    Returns: 15872.0

  25. {81,-96,12,32,68,-97}

    {-90,49,-52,-26,22,97}

    Returns: 11995.5

  26. {95,20,-14,-4,-97}

    {-95,30,47,-37,55}

    Returns: 6527.0

  27. {53,58,-74,-37}

    {-90,99,-47,38}

    Returns: 7509.0

  28. {62,-62,-63,63,-88,24,-24,88}

    {-12,12,85,-85,-94,-100,100,94}

    Returns: 46028.0

  29. {6,39,87,-87,58,-6,-58,-39}

    {-51,87,9,-9,-78,51,78,-87}

    Returns: 32106.0

  30. {-32,89,-16,-89,32,37,16,-37}

    {43,-99,71,99,-43,-25,-71,25}

    Returns: 11434.0

  31. {62,-62,48,36,-48,-4,-36,4}

    {-48,48,34,-36,-34,70,36,-70}

    Returns: 17888.0

  32. {-43,-50,50,-8,-21,8,43,21}

    {5,-42,42,60,77,-60,-5,-77}

    Returns: 16514.0

  33. {-70,-60,70,60,-67,67,-17,17}

    {88,26,-88,-26,-36,36,-62,62}

    Returns: 29318.0

  34. {-81,80,-80,81,-71,-28,71,28}

    {-71,-64,64,71,28,68,-28,-68}

    Returns: 35665.0

  35. {-27,21,27,-22,-21,22,-71,71}

    {-76,12,76,-27,-12,27,-21,21}

    Returns: 9213.0

  36. {-95,22,49,-20,95,20,-49,-22}

    {3,-17,-5,-91,-3,91,5,17}

    Returns: 18206.0

  37. {74,-28,28,-31,-62,-74,31,62}

    {27,-88,88,24,36,-27,-24,-36}

    Returns: 22943.0

  38. {53,-5,43,-48,-53,-43,48,5}

    {-89,35,-19,54,89,19,-54,-35}

    Returns: 9870.0

  39. {48,98,25,73,-98,-73,-25,-48}

    {-64,-8,28,-36,8,36,-28,64}

    Returns: 20608.0

  40. {-22,38,82,-38,-82,-60,60,22}

    {75,85,-65,-85,65,-10,10,-75}

    Returns: 33040.0

  41. {5,1,-5,-7,6,7,-1,-6}

    {51,-43,-51,35,8,-35,43,-8}

    Returns: 1862.0

  42. {65,61,63,-61,-65,-2,2,-63}

    {7,-47,-20,47,-7,-27,27,20}

    Returns: 12187.0

  43. {73,-7,-40,40,33,7,-33,-73}

    {71,53,-9,9,62,-53,-62,-71}

    Returns: 15281.0

  44. {30,80,-50,50,-80,20,-30,-20}

    {-7,-19,12,-12,19,-5,7,5}

    Returns: 70.0

  45. {-80,6,37,-43,-37,-6,43,80}

    {8,-16,4,12,-4,16,-12,-8}

    Returns: 4312.0

  46. {-79,96,-96,-17,-62,17,62,79}

    {-21,14,-14,7,-28,-7,28,21}

    Returns: 6370.0

  47. {56,-81,-25,81,-31,25,-56,31}

    {-41,44,3,-44,38,-3,41,-38}

    Returns: 5999.0

  48. {7,-7,-24,-35,24,35,5,-5}

    {-93,93,15,-34,-15,34,1,-1}

    Returns: 7667.0

  49. {-80,80,4,-28,-4,-57,57,28}

    {48,-48,-72,-93,72,-24,24,93}

    Returns: 30225.0

  50. {-63,-49,-84,84,49,26,-26,63}

    {77,-13,72,-72,13,86,-86,-77}

    Returns: 31536.0

  51. {19,81,-1,1,-19,-81,25,-25}

    {-24,-78,-47,47,24,78,81,-81}

    Returns: 17008.0

  52. {54,-91,-48,48,91,16,-16,-54}

    {80,-99,-85,85,99,-31,31,-80}

    Returns: 15874.0

  53. {62,-59,46,-62,59,-46,-49,49}

    {60,-90,44,-60,90,-44,-85,85}

    Returns: 8305.0

  54. {-36,-33,-26,26,61,36,-61,33}

    {-35,25,19,-19,-80,35,80,-25}

    Returns: 10723.0

  55. {-98,-2,89,-52,-89,98,52,2}

    {-42,-28,79,-82,-79,42,82,28}

    Returns: 19332.0

  56. {11,79,-11,-29,95,-95,-79,29}

    {36,-91,-36,-10,-23,23,91,10}

    Returns: 20326.0

  57. {-61,27,-83,-97,83,-27,61,97}

    {-100,-96,-64,-67,64,96,100,67}

    Returns: 40029.0

  58. {-42,-42,-67}

    {-93,-59,-73}

    Returns: 0.0

  59. {-1,-56,20,-72,100,-1,-85}

    {-94,-52,-48,-64,-35,-28,95}

    Returns: 0.0

  60. {-63,-65,79,25}

    {-45,-88,90,96}

    Returns: 0.0

  61. {50,13,83,49}

    {-12,-34,-14,14}

    Returns: 0.0

  62. {23,53,-21,38,62,65,-31,60}

    {22,84,40,7,-68,-9,-77,43}

    Returns: 0.0

  63. {47,33}

    {8,-14}

    Returns: 0.0

  64. {0,39,-23}

    {-82,-79,-2}

    Returns: 0.0

  65. {-76,-90,-70,57,-83,-44,-21}

    {73,98,-63,-24,-34,-74,-73}

    Returns: 0.0

  66. {91,-98,-8}

    {-14,21,-41}

    Returns: 0.0

  67. {-68,-52,71,-24,-37,7}

    {18,39,-26,-59,-2,-20}

    Returns: 0.0

  68. {0, 1, 1, -2}

    {2, -1, -1, 0}

    Returns: 2.0

    Note that we can append parallel vectors in a row. If we connect all vectors in the order they are given in the input, we get a right triangle with the hypotenuse consisting of the two (1, -1) vectors appended in a row.

  69. {1, 0, 0, 0, 0, 0, 0, -1}

    {0, 1, 1, 1, -1, -1, -1, 0}

    Returns: 3.0

  70. {0, 1, 1, 1, -1, -1, -1, 0}

    {1, 0, 0, 0, 0, 0, 0, -1}

    Returns: 3.0

  71. {2, 3, -5 }

    {2, -4, 2 }

    Returns: 7.0

  72. {25, 50, 75, 100, -25, -50, -75, -100 }

    {100, 75, 50, 25, -100, -75, -50, -25 }

    Returns: 31250.0

  73. {0, 30, 0, -30, 10, -6, 3, -7 }

    {10, 0, -10, 0, 0, -5, -5, 0 }

    Returns: 407.5

  74. {1, -1, 2, -1, 1, -2 }

    {1, 1, 0, -1, -1, 0 }

    Returns: 6.0

  75. {0, 1, 1, -2 }

    {2, -1, -1, 0 }

    Returns: 2.0

  76. {0, 2, -2, -1, 1 }

    {2, 0, 0, -1, -1 }

    Returns: 5.0

  77. {1, 1, -2, 0, 50 }

    {1, 1, 0, -2, 50 }

    Returns: 2.0

  78. {0, 0, 1, -1, 1 }

    {1, -1, 0, 0, 1 }

    Returns: 1.0

  79. {1, -1, 5, -5, 2 }

    {5, -5, 1, -1, 2 }

    Returns: 24.0

  80. {20, 20, 0, -20, -20, -60, 40, 20 }

    {40, 20, 20, 20, 0, -20, -20, -40 }

    Returns: 5000.0

  81. {1, 2, 2, -1, 2, -2, -1, 1 }

    {1, -1, 2, 1, -1, 1, -2, -1 }

    Returns: 4.5

  82. {1, -1, 1, -1, 0 }

    {1, -1, -1, 0, 1 }

    Returns: 2.5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: