Statistics

Problem Statement

Consider a N-level pyramid built of unit cubes. An example for N=3 can be seen in the image below.

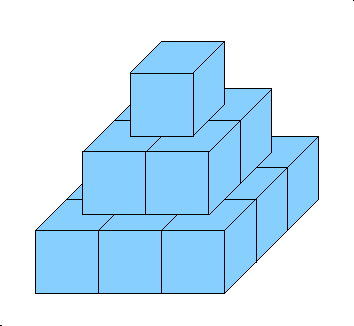
Formally, a pyramid of size N has N levels, where the i-th level (counting from the top) contains an i by i grid of unit cubes.

You have K cubes. First, you select a suitable pyramid size as follows: If K is exactly the number of cubes necessary to build a pyramid of size N for some N, you pick that size. Otherwise, you pick the smallest pyramid size you can not build.

Now you start building the pyramid in a systematic bottom-up way. First you build the complete bottom level, then you build the level above that, etc. When building a level, also proceed in a systematic way, starting the next row only when the previous one is full.

For example, for 21 cubes you should get the following incomplete pyramid:

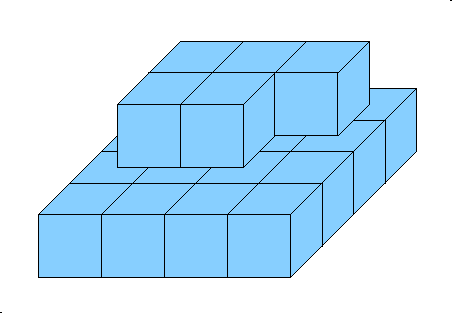
Given an int K specifying the number of cubes you have, return the surface area of the possibly incomplete pyramid you will build according to the instructions above.

Definition

Class:

PyramidOfCubes

Method:

surface

Parameters:

int

Returns:

double

Method signature:

double surface(int K)

(be sure your method is public)

Notes

• The returned value must be accurate to within a relative or absolute value of 1E-9.
• The bottom sides of the cubes on the bottommost level are a part of the surface.

Constraints

• K will be between 1 and 1,000,000,000, inclusive.

Examples

1. 14

   Returns: 42.0

   The first example from the problem statement.

2. 21

   Returns: 58.0

   The second example from the problem statement.

3. 1

   Returns: 6.0

   A single cube.

4. 2

   Returns: 10.0

   Two cubes next to each other.

5. 451234

   Returns: 47498.0

   Quite a lot of cubes.

6. 3

   Returns: 14.0

7. 4

   Returns: 16.0

8. 5

   Returns: 20.0

9. 6

   Returns: 22.0

10. 7

    Returns: 26.0

11. 8

    Returns: 28.0

12. 9

    Returns: 30.0

13. 10

    Returns: 34.0

14. 11

    Returns: 36.0

15. 12

    Returns: 38.0

16. 13

    Returns: 38.0

17. 14

    Returns: 42.0

18. 15

    Returns: 46.0

19. 16

    Returns: 48.0

20. 17

    Returns: 52.0

21. 18

    Returns: 54.0

22. 19

    Returns: 56.0

23. 20

    Returns: 58.0

24. 22

    Returns: 58.0

25. 23

    Returns: 60.0

26. 24

    Returns: 60.0

27. 25

    Returns: 60.0

28. 26

    Returns: 64.0

29. 27

    Returns: 66.0

30. 28

    Returns: 68.0

31. 29

    Returns: 68.0

32. 30

    Returns: 72.0

33. 31

    Returns: 82.0

34. 32

    Returns: 82.0

35. 33

    Returns: 82.0

36. 54406261

    Returns: 1193556.0

37. 54406260

    Returns: 1193552.0

38. 54406259

    Returns: 1193552.0

39. 54406258

    Returns: 1193550.0

40. 54406262

    Returns: 1179506.0

41. 998441521

    Returns: 8308806.0

42. 998441520

    Returns: 8308802.0

43. 998441519

    Returns: 8308802.0

44. 998441518

    Returns: 8308800.0

45. 998441500

    Returns: 8308780.0

46. 998441522

    Returns: 8252782.0

47. 998441523

    Returns: 8252782.0

48. 1000000000

    Returns: 8293536.0

49. 123456789

    Returns: 2050182.0

50. 987654321

    Returns: 8227570.0

51. 12433215

    Returns: 441910.0

52. 53253322

    Returns: 1163598.0

53. 2143565

    Returns: 135884.0

54. 547654743

    Returns: 5538756.0

55. 135784784

    Returns: 2188118.0

56. 934673245

    Returns: 7921618.0

57. 954332132

    Returns: 8024148.0

58. 123453163

    Returns: 2050094.0

59. 123

    Returns: 186.0

60. 5433

    Returns: 2466.0

61. 4

    Returns: 16.0

62. 3

    Returns: 14.0

63. 10

    Returns: 34.0

64. 6

    Returns: 22.0

65. 5

    Returns: 20.0

66. 26

    Returns: 64.0

67. 15

    Returns: 46.0

68. 9

    Returns: 30.0

69. 998441521

    Returns: 8308806.0

70. 983475384

    Returns: 8202462.0

71. 17

    Returns: 52.0

72. 1000000000

    Returns: 8293536.0

73. 25

    Returns: 60.0

74. 500000000

    Returns: 5204004.0

75. 913687900

    Returns: 7778014.0

76. 18

    Returns: 54.0

77. 7

    Returns: 26.0