Statistics

Problem Statement for "ConstructBST"

Problem Statement

This statement contains images which must be viewed in the applet.

A Binary Search Tree (BST) is a tree data structure which obeys the following properties:

  • Each node has at most 2 children.
  • Each node except the root has exactly 1 parent.
  • There is exactly 1 root node. The root node does not have any parents.
  • If a node has a left child, all values in the left subtree are less than or equal to the value of the node itself.
  • If a node has a right child, all values in the right subtree are strictly greater than the value of the node itself.

A BST is constructed from a string of characters in the following way: The root node of the tree is assigned the value of the first character in the string. All subsequent characters are added as children of existing nodes subject to the above rules. Note that the tree is never altered in any other manner. In this problem, nodes are identified starting from the root node as 1, and following in order with nodes at the next level, etc. See the figure below for clarification.

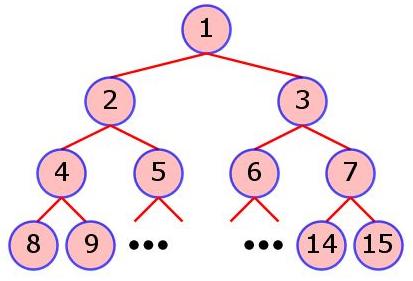
You will be given the shape of a particular BST by specifying the identities of the nodes which constitute the tree, according to the above scheme. Note that you do not know the exact input string used to construct the given BST. You do know, however, that the first N uppercase letters were used to construct the given BST with N nodes. See the examples below for further clarification.

Create a class ConstructBST that contains a method numInputs. The method takes an int[] tree with a list of node numbers present in the tree and returns a long corresponding to the number of strings composed of the characters from 'A' to 'Z' that could have been used to produce the particular BST. Note that tree will always contain a root node numbered 1. Note also, that tree will represent a connected tree, that is, all nodes present in the tree will be reachable from the root node.

Definition

Class:
ConstructBST
Method:
numInputs
Parameters:
int[]
Returns:
long
Method signature:
long numInputs(int[] tree)
(be sure your method is public)

Constraints

  • tree will contain between 1 and 26 elements, inclusive.
  • Each element of tree will be between 1 and 226-1, inclusive.
  • Each element of tree will be distinct.
  • tree will represent a connected tree.
  • tree will contain a root node numbered 1.

Examples

  1. {1, 2}

    Returns: 1

    This input represents a BST of the following shape: Using the characters {'A','B'}, only the string "BA" can generate a tree with the given shape.

  2. {1, 2, 3}

    Returns: 2

  3. {1, 3, 6}

    Returns: 1

    This input represents a BST of the following shape: Using the characters {'A','B','C'}, only the string "ACB" can generate a tree with the given shape.

  4. {1, 2, 5, 3, 4}

    Returns: 8

    Using the characters {'A','B','C','D','E'} the following 8 strings generate a tree with the given shape: "DBACE", "DBAEC", "DBEAC", "DEBAC", "DBCAE", "DBCEA", "DBECA", "DEBCA".

  5. {1,2,4,8,16,32,64,128,256,512,1024,2048,4096}

    Returns: 1

  6. {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}

    Returns: 319258368000

  7. {1, 2, 3, 4, 8, 9, 6, 7, 12, 24, 25, 14, 15, 50, 51, 31, 62, 124, 125, 250}

    Returns: 3910915008

  8. {1, 2, 3, 4, 8, 9, 6, 7, 12, 24, 25, 14, 15, 50, 51, 31, 62, 124, 125, 250, 501}

    Returns: 12415603200

  9. {1, 2, 3, 4, 6, 7, 12, 25, 14, 15, 50, 51, 31, 62, 124, 125, 250}

    Returns: 6486480

  10. {2, 4, 3, 63, 7, 15, 1, 31, 5}

    Returns: 112

  11. {1,2,4,8,16,32,64,128,256,512,1024,2048,4096, 513}

    Returns: 5

  12. {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192}

    Returns: 1

  13. {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,3,7,15,31,63,127,255,511}

    Returns: 203490

  14. {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,3,7,15,31,63,127,255,511,5,16384,32768,32769}

    Returns: 34610400

  15. {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26}

    Returns: 241240136417280000

  16. {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,31}

    Returns: 217116122775552000

  17. {1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18,19,20,21,22,23,31,62,63,126}

    Returns: 46524883451904000

  18. {1,20,21,22,23,24,25,26,27,10,11,12,13,5,6,2,3}

    Returns: 82368000

  19. {1,10,11,12,13,5,6,2,3}

    Returns: 280

  20. {1,20,21,22,23,24,25,26,27,10,11,12,13,5,6,2,3,4,8,9,7,14,15}

    Returns: 260050452480000

  21. {1,2,4,9,18,37,74,148,296,592,3,7,14,29,58,117,235,471,943,1887}

    Returns: 92378

  22. {1,2,4,9,18,37,74,148,296,592,3,7,14,29,58,117,235,471,943,1887,3774,7548,15096,30192,60384,120769}

    Returns: 2042975

  23. {1,2,4,9,18,37,74,148,296,592,3,6,12,7,14,29,58,117,235,471,943,1887,3774,7548,15096,30192}

    Returns: 214512375

  24. {1,2,4,9,18,37,74,148,296,592,3,6,5,7,14,29,58,117,235,471,943,1887,3774,7548,15096,30192}

    Returns: 411863760

  25. {1}

    Returns: 1

  26. {1,2,3,4,6,13,27,54,55,8,17,16,34,35,68,69,70,71}

    Returns: 15841280

  27. {1,2,3,4,6,13,27,54,55,8,17,16,34,35,68,69,70,71,136,137,274,275,548,549,550,551}

    Returns: 26404618240000

  28. {1,2,3,4,6,13,27,54,55,8,17,16,34,35,68,69,70,71,12,24,25,50,51}

    Returns: 910176583680

  29. {1,2,3,4,6,13,27,54,55,8,17,16,34,35,68,69,70,71,12,24,25,50,51,5,10,11}

    Returns: 3289638223872000

  30. {1,2,3,4,6,13,27,54,55,8,17,16,34,35,68,69,70,71,12,24,25,50,51,111,223,447}

    Returns: 90374676480000

  31. {1,2,4,5,8,9,16,17,32,33,64,65,128,129,256,257,512,513,1024,1025,2048,2049,4096,4097}

    Returns: 81749606400

  32. {1,2,4,5,8,9,16,17,32,33,64,65,128,129,256,257,512,513,1024,1025,2048,2049,4096,4097,8193}

    Returns: 316234143225

  33. {1,2,3,4,5,8,9,16,17,32,33,64,65,128,129,256,257,512,513,1024,1025,2048,2049,4096,4097}

    Returns: 1961990553600

  34. {1,2,4,5,8,9,16,17,32,33,64,65,128,129,3,6,7,14,15,30,31,62,63,126,127}

    Returns: 441685691596800

  35. {1,2,4,5,8,9,16,17,32,33,64,65,128,129,3,6,7,14,15,30,31,62,63,126,127,10}

    Returns: 5126708920320000

  36. {1,2,4,5,8,9,16,17,32,33,64,65,128,129,3,6,7,14,15,30,31,62,63,126,127,11}

    Returns: 5126708920320000

  37. {1,2,4,5,8,9,16,17,32,33,64,65,128,129,3,6,7,14,15,30,31,62,63,126,127,12}

    Returns: 5060981882880000

  38. {1,2,3,4,6,7,8}

    Returns: 40

  39. {1,2,3,4,6,7,8,12,14,16,24,28,32,48,56,64,96,112,128,192,224,256}

    Returns: 188024760

  40. {1,2,4,9,18,37,74,148,296,592,3,7,14,29,58,117,235,471,943,1887,1886}

    Returns: 335920

  41. {1,2,4,9,18,37,74,148,3,7,14,29,58,117,235,471,943,1886}

    Returns: 19448

  42. {1,2,4,5,9,18,37,74,148,3,7,14,29,58,117,235,471,943,1886}

    Returns: 306306

  43. {1,2,4,9,18,37,74,148,3,7,14,29,58,117,235,471,943,1886,75}

    Returns: 131274

  44. {1,2,4,9,18,37,74,148,3,7,14,29,58,117,235,471,943,1886,75,151,302}

    Returns: 1847560

  45. {1,2,4,5,8,9,16,17,32,33,64,65,3,6,7,14,15,30,31,62,63,10}

    Returns: 2383795814400

  46. {1,2,4,5,8,9,16,17,32,33,3,6,7,14,15,30,31,10}

    Returns: 1613094912

  47. {1,2,4,5,8,9,16,17,3,6,7,14,15,30,31,62,63,10}

    Returns: 1568286720

  48. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,131070}

    Returns: 2

  49. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 16777215, 33554431, 67108863}

    Returns: 1

  50. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 16777215, 33554431, 33554430}

    Returns: 2

  51. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 16777215, 33554431, 2}

    Returns: 25

  52. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 16777215, 2, 4}

    Returns: 300

  53. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 16777215, 2, 6}

    Returns: 575

  54. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 13, 2, 6}

    Returns: 6325

  55. {1,3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607, 14, 2, 6}

    Returns: 12075

  56. {100,50,25,12,6,3,1}

    Returns: 1

  57. {100,50,25,12,6,3,1,2,4,8,16,32,33}

    Returns: 1848

  58. {100,50,25,12,6,3,1,2,4,8,16,5}

    Returns: 1848

  59. {100,50,25,12,6,3,1,2,4,8,16,5,200,400,800,1600,3200,6400,12800,12801}

    Returns: 93024

  60. {125115, 62557, 31278, 15639, 7819, 3909, 1954, 977, 488, 244, 122, 61, 30, 15, 7, 3, 1, 2, 4}

    Returns: 153

  61. {125115, 62557, 31278, 15639, 7819, 3909, 1954, 977, 488, 244, 122, 61, 30, 15, 7, 3, 1, 2, 5, 11, 23}

    Returns: 4845

  62. {125115, 62557, 31278, 15639, 7819, 3909, 1954, 977, 488, 244, 122, 61, 30, 15, 7, 3, 1, 2}

    Returns: 17

  63. {283561, 141780, 70890, 35445, 17722, 8861, 4430, 2215, 1107, 553, 276, 138, 277, 69, 34, 17, 8, 4, 2, 1, 9}

    Returns: 216

  64. {283561, 141780, 70890, 35445, 17722, 8861, 4430, 2215, 1107, 553, 276, 138, 69, 34, 17, 8, 4, 2, 1, 3, 7}

    Returns: 190

  65. {283561, 141780, 70890, 35445, 17722, 8861, 4430, 2215, 1107, 1106, 553, 276, 138, 69, 34, 17, 8, 4, 2, 1, 3}

    Returns: 200

  66. {1, 2, 4, 6, 3}

    Returns: 6

  67. {2, 4, 3, 62, 7, 15, 1, 31, 5, 14, 28, 57, 56, 114}

    Returns: 96096

  68. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 45, 90 }

    Returns: 706758212160000

  69. {2, 4, 3, 62, 7, 15, 1, 31, 5, 14, 28, 57, 56, 114 }

    Returns: 96096

  70. {1, 3, 2, 6, 5, 10, 11, 12, 13, 20, 21, 40, 41, 80, 81, 82, 83, 160, 320, 640, 1280, 2560, 5120 }

    Returns: 11535462400

  71. {14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 }

    Returns: 241240136417280000

  72. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 }

    Returns: 241240136417280000

  73. {1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 6, 12, 24, 48, 49, 97 }

    Returns: 24024

  74. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 24, 25, 26, 28, 29 }

    Returns: 142076522649600000

  75. {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 3 }

    Returns: 25

  76. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 40, 41 }

    Returns: 186251575910400000

  77. {1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575, 2097151, 4194303, 8388607, 16777215, 33554431, 67108863 }

    Returns: 1

  78. {25, 2, 14, 3, 11, 4, 5, 6, 13, 1, 8, 10, 22, 12, 16, 9, 17, 18, 15, 20, 7, 21, 19, 23, 24, 26 }

    Returns: 241240136417280000

  79. {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 16777217 }

    Returns: 2

  80. {1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191, 16383, 32767, 65535, 131071, 262143, 524287, 1048575 }

    Returns: 1

  81. {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 513 }

    Returns: 2

  82. {1, 3, 2, 4, 5, 8, 9, 10, 11, 16, 17, 18, 19, 20, 21, 22, 23, 32, 33, 34, 35, 36, 37, 38, 39, 40 }

    Returns: 56540656972800000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2024, TopCoder, Inc. All rights reserved.
This problem was used for: