Statistics

Problem Statement

This problem statement contains an image that may not display properly if viewed outside of the applet.

You play a game with your friend in which 16 square pieces are placed in a 4x4 grid on a board. Each piece has a distinct number between 1 and 16 written on it. A piece can be removed from the board if it is on an edge or if it can be dragged left, right, up or down through a path of unoccupied squares, until it leaves the board. When a piece is removed from the board, the square it occupied becomes unoccupied.

On the board below, all pieces can be removed from the board. For example, the selected piece can be dragged one square down, then one square left, and finally it can be removed from the board by dragging it down:

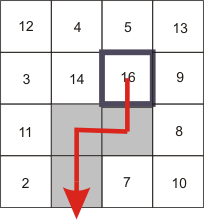
You take alternate turns removing pieces from the board until all of them are removed. The score of each player is calculated by summing the values of the pieces he has removed. Each player follows an optimal strategy that maximizes the difference between his score and his opponent's score. You are the first to move.

You will be given a String[] board. Each element of board contains four integers separated by single spaces. The jth integer in the ith element of board represents the number written on the piece in the ith row and jth column of the grid. Return the maximum possible score difference between you and your friend, assuming both of you play optimally.

Definition

Class:

ScoreDifference

Method:

maximize

Parameters:

String[]

Returns:

int

Method signature:

int maximize(String[] board)

(be sure your method is public)

Constraints

• board will contain exactly 4 elements.
• Each element of board will contain exactly four positive integers, with no leading zeroes, separated by single spaces, and will contain no leading or trailing spaces.
• Each integer between 1 and 16 will appear exactly once in board.

Examples

1. {"12 4 5 13", "3 14 16 9", "11 6 15 8", "2 1 7 10"}

   Returns: 2

   It is not always best to remove the piece with the highest point value. On the first turn you can remove any piece except the four middle ones. The best option is to remove the piece in the upper right corner. Your friend will then choose the piece from the upper left corner. It is still not possible to remove the middle four pieces. You go on by removing the 11 point piece and the piece valued 6 can now be removed. Your friend will remove the piece in the bottom right corner. At this point you have an advantage of 2 points. The piece with the highest value that can now be removed is the 9 piece. If you remove this one, the remaining pieces will be removed in the order 16, 15, 14, 8, 7, 6, 5, 4, 3, 2, 1 and you will end up in a draw game. However, if you remove the 8 piece, the remaining pieces will be removed in the order 8, 15, 16, 14, 9, 7, 6, 5, 4, 3, 2, 1 and you will keep the 2 point advantage.

2. {"15 16 11 12", "10 13 4 7", "1 2 8 6", "9 5 3 14"}

   Returns: 6

3. {"6 8 1 16", "10 15 9 3", "2 5 7 14", "13 12 11 4"}

   Returns: 10

4. {"9 8 3 1", "10 6 15 5", "12 7 4 11", "14 13 16 2"}

   Returns: 16

5. {"12 8 6 5","2 11 9 15","13 10 14 7","1 16 4 3"}

   Returns: 4

6. {"7 2 8 4","3 16 10 12","9 6 14 11","15 13 1 5"}

   Returns: 8

7. {"4 10 14 3","2 7 15 6","11 1 13 9","5 8 16 12"}

   Returns: 10

8. {"9 6 2 10","5 11 3 8","16 1 12 13","14 15 7 4"}

   Returns: 12

9. {"15 10 12 11","6 3 4 13","14 5 16 1","9 8 7 2"}

   Returns: 16

10. {"11 9 3 4","1 16 8 13","14 10 6 5","7 15 12 2"}

    Returns: 14

11. {"7 3 13 12","1 5 2 15","8 4 6 14","9 16 11 10"}

    Returns: 10

12. {"3 11 7 15","14 4 16 2","8 13 1 6","10 12 5 9"}

    Returns: 14

13. {"7 14 6 16","9 11 5 4","2 12 8 3","15 1 13 10"}

    Returns: 6

14. {"8 6 1 4","3 7 16 2","11 15 5 9","14 10 13 12"}

    Returns: 12

15. {"13 8 7 15","6 14 10 1","11 9 12 5","2 3 4 16"}

    Returns: 6

16. {"5 9 15 6","2 8 3 12","14 16 11 1","13 7 4 10"}

    Returns: 8

17. {"7 2 6 5","1 13 3 11","16 4 9 10","14 8 12 15"}

    Returns: 18

18. {"14 10 8 7","16 2 12 4","15 6 3 9","1 5 13 11"}

    Returns: 8

19. {"6 15 16 7","14 5 12 13","1 11 2 9","3 4 10 8"}

    Returns: 12

20. {"15 11 7 12","2 3 8 14","16 13 9 6","4 5 1 10"}

    Returns: 8

21. {"11 8 13 12","1 14 9 6","7 10 4 3","5 2 16 15"}

    Returns: 12

22. {"13 12 1 4","2 7 9 6","11 5 8 15","3 16 14 10"}

    Returns: 10

23. {"2 3 12 7","6 16 5 15","14 4 9 8","13 10 11 1"}

    Returns: 16

24. {"9 11 14 3","5 6 2 4","12 13 16 7","1 15 8 10"}

    Returns: 6

25. {"7 10 13 8","16 12 5 4","14 3 15 2","11 6 9 1"}

    Returns: 10

26. {"9 3 6 13","1 14 2 4","7 5 11 10","8 12 16 15"}

    Returns: 16

27. {"14 5 16 13","8 9 3 11","7 1 12 4","2 10 6 15"}

    Returns: 12

28. {"2 15 10 6","13 5 1 16","11 8 3 4","7 14 12 9"}

    Returns: 8

29. {"9 4 11 10","2 12 3 13","6 1 16 15","8 5 7 14"}

    Returns: 14

30. {"11 16 9 13","1 2 4 12","7 10 6 5","8 3 15 14"}

    Returns: 6

31. {"13 6 3 12","16 4 14 5","11 7 1 10","8 15 9 2"}

    Returns: 14

32. {"6 5 15 4","10 14 2 8","3 7 12 9","11 16 13 1"}

    Returns: 8

33. {"10 12 9 7","13 11 6 8","16 1 14 4","3 15 5 2"}

    Returns: 16

34. {"2 9 13 1","8 15 5 11","16 12 3 14","6 4 7 10"}

    Returns: 10

35. {"11 4 5 13","3 14 15 9","12 8 16 6","2 1 7 10"}

    Returns: 2

36. {"4 10 3 11","14 2 15 7","16 13 5 6","1 8 9 12"}

    Returns: 12

37. {"10 9 1 5","12 11 4 13","14 8 7 16","3 2 15 6"}

    Returns: 8

38. {"10 3 8 4","14 7 16 1","11 12 6 5","15 9 13 2"}

    Returns: 16

39. {"7 3 8 10","9 4 16 6","12 11 1 14","13 15 5 2"}

    Returns: 14

40. {"12 13 8 4","5 3 14 9","2 6 7 16","10 1 11 15"}

    Returns: 4

41. {"4 3 16 13","6 10 9 7","11 12 1 15","2 5 14 8"}

    Returns: 6

42. {"8 5 14 9","2 12 7 6","15 4 13 3","16 1 11 10"}

    Returns: 14

43. {"9 8 3 1", "10 6 15 5", "12 7 4 11", "14 13 16 2" }

    Returns: 16

44. {"15 16 11 12", "10 13 4 7", "1 2 8 6", "9 5 3 14" }

    Returns: 6