Statistics

Problem Statement

Given a rectangular grid where all the cells are initially white, you perform the following procedure K times:

• Select a cell from the grid at random, and call it A
• Select a cell from the grid at random, and call it B
• Color all the cells in the rectangle bounded by A and B

Each cell is selected at random, with uniform distribution, and each selection is independent from the other selections. It's possible that A and B correspond to the same cell.

For example, the image below shows a 5x7 grid where the selected pairs could have been (row, column):

• (0,1); (3,2)
• (3,6); (4,0)
• (0,6); (0,5)

Resulting in a grid with 22 colored cells and 13 white cells.

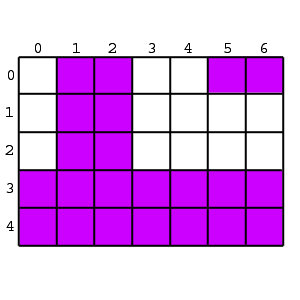
You are given ints rows and cols, the dimensions of the grid. Return the expected number of colored cells after K steps.

Definition

Class:

GridColoring

Method:

area

Parameters:

int, int, int

Returns:

double

Method signature:

double area(int K, int rows, int cols)

(be sure your method is public)

Notes

• The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

• K will be between 0 and 100, inclusive.
• rows will be between 1 and 1000, inclusive.
• cols will be between 1 and 1000, inclusive.

Examples

1. 1

   2

   1

   Returns: 1.5

   The grid has two cells. The probability that both of them will get colored is 0.5, and the probability that only one of them will get colored is 0.5. So the expected value is 0.5 * 2 + 0.5 * 1 = 1.5.

2. 2

   2

   1

   Returns: 1.875

   With the same grid as in the previous example, but two selections, the expected value rises to 1.875.

3. 1

   2

   2

   Returns: 2.25

4. 3

   5

   7

   Returns: 19.11917924647044

5. 0

   1000

   1000

   Returns: 0.0

6. 0

   1

   1

   Returns: 0.0

7. 1

   1

   1

   Returns: 1.0

8. 100

   1000

   1000

   Returns: 936523.8255150901

9. 100

   10

   10

   Returns: 99.88968353731948

10. 10

    1

    1000

    Returns: 899.4762927482861

11. 1

    1000

    1000

    Returns: 111778.55488900792

12. 1

    134

    735

    Returns: 11233.367350323373

13. 32

    407

    341

    Returns: 116240.54757560963

14. 22

    746

    624

    Returns: 361402.1850454167

15. 74

    481

    873

    Returns: 385866.8707868741

16. 10

    670

    441

    Returns: 177326.4195460204

17. 37

    471

    402

    Returns: 161949.78168659535

18. 9

    519

    871

    Returns: 258187.2031884151

19. 50

    164

    158

    Returns: 23216.23645834032

20. 54

    3

    962

    Returns: 2800.7937506029925

21. 77

    412

    452

    Returns: 171908.35227779343

22. 56

    911

    898

    Returns: 732873.967598473

23. 93

    952

    24

    Returns: 21901.47306437352

24. 13

    15

    644

    Returns: 7069.852152955285

25. 46

    718

    798

    Returns: 502817.0384180637

26. 23

    717

    872

    Returns: 489988.86053183925

27. 84

    383

    145

    Returns: 51844.25256408814

28. 100

    469

    638

    Returns: 280743.0367106806

29. 61

    493

    214

    Returns: 95769.7553567456

30. 34

    953

    283

    Returns: 227809.7925184241

31. 62

    296

    339

    Returns: 91185.11247572151

32. 16

    931

    253

    Returns: 168609.67907692306

33. 38

    119

    104

    Returns: 10798.035487868288

34. 72

    890

    331

    Returns: 270404.5665187198

35. 90

    681

    95

    Returns: 60796.88953290993

36. 76

    277

    271

    Returns: 69429.47695878157

37. 48

    830

    282

    Returns: 206929.07822313998

38. 69

    951

    561

    Returns: 487332.92756517127

39. 86

    651

    801

    Returns: 484143.02860733605

40. 78

    257

    88

    Returns: 21122.560270693717

41. 1

    391

    519

    Returns: 22851.76731270509

42. 42

    922

    600

    Returns: 480176.35327794595

43. 14

    47

    137

    Returns: 4585.930861526224

44. 82

    912

    804

    Returns: 678227.2050009246

45. 13

    437

    59

    Returns: 17640.45548961717

46. 9

    641

    223

    Returns: 82124.0608682331

47. 66

    790

    503

    Returns: 361807.85022047587

48. 20

    712

    133

    Returns: 72495.90542539785

49. 69

    461

    170

    Returns: 71997.75342052174

50. 96

    17

    18

    Returns: 303.30323071359965

51. 70

    453

    347

    Returns: 144117.5323233712

52. 92

    43

    279

    Returns: 11421.814504595835

53. 64

    131

    165

    Returns: 19854.00407011627

54. 11

    921

    127

    Returns: 73803.89125808806

55. 7

    703

    640

    Returns: 225867.55102845063

56. 62

    715

    270

    Returns: 175182.88030002217

57. 50

    1000

    900

    Returns: 796768.2637934526

58. 99

    999

    999

    Returns: 934096.6601304637

59. 100

    1

    2

    Returns: 2.0

60. 45

    324

    999

    Returns: 283804.85143968154